
ЁОЬтФПЁПдкЧѓ1+3+32+33+34+35+36+37+38ЕФжЕЪБЃЌРюУєЗЂЯжЃКДгЕкЖўИіМгЪ§Ц№УПвЛИіМгЪ§ЖМЪЧЧАвЛИіМгЪ§ЕФ3БЖЃЌгкЪЧЫ§МйЩшЃК
SЃН1+3+32+33+34+35+36+37+38Ђй
ШЛКѓдкЂйЪНЕФСНБпЖМГЫ3ЃЌЕУЃЌ
3SЃН3+32+33+34+35+36+37+38+39Ђк
ЂкЉЂйЕУЃЌ3SЉSЃН39Љ1ЃЌМД2SЃН39Љ1ЃЌ
ЫљвдSЃН![]()
ЧыАЎЖЏФдНюЕФФуЧѓГі1+5+52+53+54+Ё+52019ЕФжЕЃЎ
е§ШЗД№АИЪЧ_____ЃЎ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНxЃ2гыyжсЯрНЛгкЕуAЃЌгыЗДБШР§КЏЪ§yЃН![]() дкЕквЛЯѓЯоФкЕФЭМЯѓЯрНЛгкЕуB(mЃЌ2)ЃЎ
дкЕквЛЯѓЯоФкЕФЭМЯѓЯрНЛгкЕуB(mЃЌ2)ЃЎ
(1)ЧѓИУЗДБШР§КЏЪ§ЕФЙиЯЕЪНЃЛ
(2)ШєжБЯпyЃНxЃ2ЯђЩЯЦНвЦКѓгыЗДБШР§КЏЪ§yЃН![]() дкЕквЛЯѓЯоФкЕФЭМЯѓЯрНЛгкЕуCЃЌЧвЁїABCЕФУцЛ§ЮЊ18ЃЌЧѓЦНвЦКѓЕФжБЯпЖдгІЕФКЏЪ§ЙиЯЕЪНЃЎ
дкЕквЛЯѓЯоФкЕФЭМЯѓЯрНЛгкЕуCЃЌЧвЁїABCЕФУцЛ§ЮЊ18ЃЌЧѓЦНвЦКѓЕФжБЯпЖдгІЕФКЏЪ§ЙиЯЕЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮжНЦЌABCDЃЌAB=9ЃЌBC=6ЃЌдкОиаЮБпЩЯгавЛЕуPЃЌЧвDP=3ЃЎНЋОиаЮжНЦЌелЕўЃЌЪЙЕуBгыЕуPжиКЯЃЌелКлЫљдкжБЯпНЛОиаЮСНБпгкЕуEЃЌFЃЌдђEFГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫДгМзЁЂввСНУћЭЌбЇжабЁАЮвЛШЫВЮМгЩфЛїБШШќЃЌдкЭЌЕШЕФЬѕМўЯТЃЌНЬСЗИјМзЁЂввСНУћЭЌбЇАВХХСЫвЛДЮЩфЛїВтбщЃЌУПШЫДђ10ЗЂзгЕЏЃЎЯТБэЪЧМзЁЂввСНШЫИїздЕФЩфЛїЧщПіМЧТМ(ЦфжаввЕФМЧТМБэЩЯЩфжа9ЃЌ10ЛЗЕФзгЕЏЪ§БЛФЋЫЎЮлШОПДВЛЧхГўЃЌЕЋЪЧНЬСЗМЧЕУввЩфжа9ЃЌ10ЛЗЕФзгЕЏЪ§ОљВЛЮЊ0ЗЂ)ЃЎ
Мз
жаАаЛЗЪ§(ЛЗ) | 5 | 6 | 8 | 9 | 10 |
ЩфжаДЫЛЗЕФзгЕЏЪ§(ЗЂ) | 4 | 1 | 3 | 1 | 1 |
вв
жаАаЛЗЪ§(ЛЗ) | 5 | 6 | 7 | 9 | 10 |
ЩфжаДЫЛЗЕФзгЕЏЪ§(ЗЂ) | 2 | 3 | 2 |
(1)ЧѓМзЭЌбЇдкетДЮВтбщжаЦНОљУПДЮЩфжаЕФЛЗЪ§ЃЛ
(2)ДгетДЮВтбщЕФЦНОљГЩМЈЕФНЧЖШПМТЧЃЌШчЙћФуЪЧНЬСЗЃЌФуШЯЮЊбЁЫВЮМгБШШќБШНЯКЯЪЪЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ 1ЃЌЩфЯп OCдкЁЯAOBЕФФкВПЃЌЭМжаЙВга 3ИіНЧЃКЁЯAOBЁЂЁЯAOC КЭЁЯBOCЃЌШєЦфжагавЛИіНЧЕФЖШЪ§ЪЧСэвЛИіНЧЖШЪ§ЕФСНБЖЃЌдђГЦЩфЯп OCЪЧЁЯAOBЕФЦцУюЯпЃЎ
ЃЈ1ЃЉвЛИіНЧЕФНЧЦНЗжЯп_______етИіНЧЕФЦцУюЯпЃЎЃЈЬюЪЧЛђВЛЪЧЃЉЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌШєЁЯMPNЃН60ЁуЃЌЩфЯп PQШЦЕу PДг PNЮЛжУПЊЪМЃЌвдУПУы 10ЁуЕФЫйЖШФцЪБеыа§зЊЃЌЕБЁЯQPNЪзДЮЕШгк 180ЁуЪБЭЃжЙа§зЊЃЌЩша§зЊЕФЪБМфЮЊ tЃЈsЃЉЃЎ
Ђй ЕБ tЮЊКЮжЕЪБЃЌЩфЯп PMЪЧЁЯQPN ЕФЦцУюЯпЃП

ЂкШєЩфЯп PM ЭЌЪБШЦЕу PвдУПУы 5ЁуЕФЫйЖШФцЪБеыа§зЊЃЌВЂгы PQЭЌЪБЭЃжЙа§зЊЃЎЧыЧѓГіЕБЩфЯп PQЪЧЁЯMPNЕФЦцУюЯпЪБ tЕФжЕЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИіГЄЗНЬхжНКаЕФЦНУцеЙПЊЭМЃЌвбжЊжНКажаЯрЖдСНИіУцЩЯЕФЪ§ЛЅЮЊЯрЗДЪ§ЃЎ
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЯШЛЏМђЃЌдйЧѓжЕЃК5a2bЉ[2a2bЉ3ЃЈ2abcЉa2bЃЉ]+4abcЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
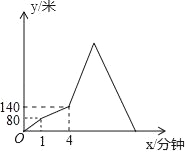
ЁОЬтФПЁПМзЁЂввСНШЫДгAЕиГіЗЂЧАЭљBЕиЃЌМзЯШГіЗЂ1ЗжжгКѓЃЌввдйГіЗЂЃЌввГіЗЂвЛЖЮЪБМфКѓЗЕЛиAЕиШЁЮяЦЗЃЌМзЁЂввСНШЫЭЌЪБДяЕНBЕиКЭAЕиЃЌВЂСЂМДЕєЭЗЯрЯђЖјаажБжСЯргіЃЌМзЁЂввСНШЫжЎМфЯрОрЕФТЗГЬyЃЈУзЃЉгыМзГіЗЂЕФЪБМфxЃЈЗжжгЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌдђМзЁЂввСНШЫзюКѓЯргіЪБЃЌввОрBЕиЕФТЗГЬЪЧ_____УзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
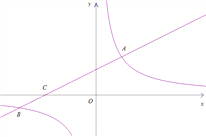
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() ЯрНЛгкЕуAЃЈmЃЌ3ЃЉЃЌB(-6ЃЌn)ЃЌгыxжсНЛгкЕуCЃЎ
ЯрНЛгкЕуAЃЈmЃЌ3ЃЉЃЌB(-6ЃЌn)ЃЌгыxжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPдкxжсЩЯЃЌЧв![]() ЃЌЧѓЕуPЕФзј БъЃЈжБНгаДГіНсЙћЃЉЃЎ
ЃЌЧѓЕуPЕФзј БъЃЈжБНгаДГіНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкгааЉЧщПіЯТЃЌВЛашвЊМЦЫуГіНсЙћвВФмАбОјЖджЕЗћКХШЅЕєЃЎР§ШчЃК
|6ЃЋ7|ЃН6ЃЋ7ЃЛ|6Ѓ7|ЃН7Ѓ6ЃЛ|7Ѓ6|ЃН7Ѓ6ЃЛ|Ѓ6Ѓ7|ЃН6ЃЋ7ЃЛ
ИљОнЩЯУцЕФЙцТЩЃЌАбЯТСаИїЪНаДГЩШЅЕєОјЖджЕЗћКХЕФаЮЪНЃК
(1)|7Ѓ21|ЃН_________ЃЛ
(2)|-![]() +0.8|ЃН____________ЃЛ
+0.8|ЃН____________ЃЛ
(3)|![]() |ЃН__________ЃЛ
|ЃН__________ЃЛ
(4)гУКЯРэЕФЗНЗЈМЦЫуЃК|![]() |ЃЋ|
|ЃЋ|![]() |-|Ѓ
|-|Ѓ![]() |Ѓ
|Ѓ![]() ЁС|-
ЁС|-![]() |ЃЋ
|ЃЋ![]() .
.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com