
【题目】如图 1,射线 OC在∠AOB的内部,图中共有 3个角:∠AOB、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线 OC是∠AOB的奇妙线.
(1)一个角的角平分线_______这个角的奇妙线.(填是或不是);
(2)如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).
① 当 t为何值时,射线 PM是∠QPN 的奇妙线?

②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转,并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.


【答案】(1)是;(2) ①当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线;②当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.
【解析】
(1)根据奇妙线定义即可求解;
(2)①分3种情况,根据奇妙线定义列方程求解即可;
②分3种情况,根据奇妙线定义列方程求解即可.
解:(1) 一个角的平分线是这个角的“奇妙线”;
(2) ①∠MPN=60,∠QPM=10t-60,∠QPN=10t(最大角),
当∠MPN=2∠QPM时,60=2(10t-60),解得t=9;
当∠QPN=2∠MPN时,10t =2×60,解得t=12;
当∠QPM=2∠MPN时,10t-60=2×60,解得t=18;
综上,当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线.
②∠QPN=10t,∠QPM=60-10t+5t=60-5t,∠MPN=60+5t(最大角),
当∠QPM=2∠QPN时, 60-5t =2×10t ,解得t=![]() ;
;
当∠MPN=2∠QPN时,60+5t =2×10t,解得t=4;
当∠QPN=2∠QPM时,10t =2×(60-5t),解得t=6;
综上,当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.
故答案为:(1)是;(2) ①当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线;②当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.


科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线m:y=﹣2x2﹣2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
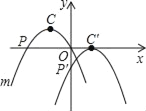
A. C(﹣![]() ,
,![]() ) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣
) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,线段AC=8cm,BC=4cm,点M、N分别是AC、BC的中点, 求:
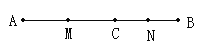
(1) 线段MN的长度.
(2) 根据(1)的计算过程和结果,设AC+BC=![]() ,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数![]() 至
至![]() 按照一定规律排成下表:
按照一定规律排成下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…… |
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第
表示第![]() 行第
行第![]() 个数是
个数是![]() .
.
(1)直接写出![]() _______________,
_______________,![]() _______________;
_______________;
(2)①如果![]() ,那么
,那么![]() _________________,
_________________,![]() ________;②用
________;②用![]() ,
,![]() 表示
表示![]() __________;
__________;
(3)将表格中的![]() 个阴影格子看成一个整体并平移,所覆盖的
个阴影格子看成一个整体并平移,所覆盖的![]() 个数之和能否等于
个数之和能否等于![]() .若能,求出这
.若能,求出这![]() 个数中的最小数,若不能说明理由.
个数中的最小数,若不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,李敏发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:
S=1+3+32+33+34+35+36+37+38①
然后在①式的两边都乘3,得,
3S=3+32+33+34+35+36+37+38+39②
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S=![]()
请爱动脑筋的你求出1+5+52+53+54+…+52019的值.
正确答案是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
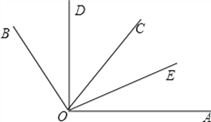
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,AD∥BC,过B作BE⊥AD交AD于点E,AB=13cm,BC=21cm,AE=5cm.动点P从点C出发,在线段CB上以每秒1cm的速度向点B运动,动点Q同时从点A出发,在线段AD上以每秒2cm的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动,设运动的时间为t(秒)
(1)当t为何值时,四边形PCDQ是平行四边形?
(2)当t为何值时,△QDP的面积为60cm2?
(3)当t为何值时,PD=PQ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com