
【题目】如图所示,点D是等腰Rt△ABC的斜边BC上一动点,连接AD,作等腰Rt△ADE,使AD=AE,且∠DAE=90°连接BE、CE.

(1)判断BD与CE的数量关系与位置关系,并进行证明;
(2)当四边形ADCE的周长最小值是6时,求BC的值.
【答案】(1)BD=CE,BD⊥CE;理由见解析;(2)BC=3.
【解析】
(1)利用SAS证出△ABD≌△ACE,然后根据全等三角形的性质和等腰直角三角形的性质即可求出结论;
(2)根据周长公式即可求出,四边形ADCE的周长=2AD+BC,其中BC为定值,四边形ADCE的周长最小,即AD最小,当AD⊥BC时,根据垂线段最短,此时AD最小,则四边形ADCE的周长最小,根据三线合一和直角三角形斜边上的中线等于斜边的一半,可得AD=![]() BC,从而求出BC.
BC,从而求出BC.
解:(1)BD=CE,BD⊥CE;
理由:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE=45°,
∵∠ACB=45°,
∴∠BCE=90°,
∴BD⊥CE;
(2)∵四边形ADCE的周长=AD+AE+CE+CD=2AD+BD+CD=2AD+BC,其中BC为定值,
∴四边形ADCE的周长最小,即AD最小,
当AD⊥BC时,根据垂线段最短,此时AD最小,则四边形ADCE的周长最小,
∵△ABC为等腰三角形,AD⊥BC
∴AD=![]() BC
BC
∴此时四边形ADCE的周长= 2AD+BC=2×![]() BC+BC=6
BC+BC=6
解得:BC=3.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)4+(-2)=_____________; (2)-3-(-2)=__________;
(3)-2×5=_____________; (4)-6÷(-3)=__________;
(5)![]() =_____________; (6)
=_____________; (6)![]() =__________;
=__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
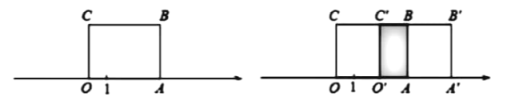
【题目】如图1,长方形![]() 的边
的边![]() 在数轴上,
在数轴上,![]() 为原点,长方形
为原点,长方形![]() 的面积为12,
的面积为12,![]() 边的长为3.
边的长为3.
(1)数轴上点![]() 表示的数为________.
表示的数为________.
(2)将长方形![]() 沿数轴水平移动,移动后的长方形记为
沿数轴水平移动,移动后的长方形记为![]() ,设长方形
,设长方形![]() 移动的距离为
移动的距离为![]() ,移动后的长方形
,移动后的长方形![]() 与原长方形
与原长方形![]() 重叠部分的面积记为
重叠部分的面积记为![]() .
.
①当![]() 等于原长方形
等于原长方形![]() 面积的
面积的![]() 时,则点
时,则点![]() 的移动距离
的移动距离![]() _______,此时数轴上点
_______,此时数轴上点![]() 表示的数为_______.
表示的数为_______.
②![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 当点
当点![]() ,
,![]() 所表示的数互为相反数时,则
所表示的数互为相反数时,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
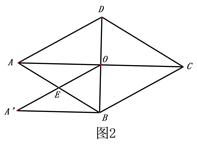
【题目】如图1,菱形ABCD,AB=4,∠ADC=120o,连接对角线AC、BD交于点O,
(1)如图2,将△AOD沿DB平移,使点D与点O重合,求平移后的△A′BO与菱形ABCD重合部分的面积.
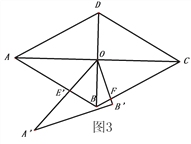
(2)如图3,将△A′BO绕点O逆时针旋转交AB于点E′,交BC于点F,
①求证:BE′+BF=2,
②求出四边形OE′BF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y=![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=![]() 的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=
的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=![]() ,则k2-k1的值为( )
,则k2-k1的值为( )

A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A、O、E三点在同一条直线上,∠AOB=∠COD=90°,观察图形后有以下四个结论,其中正确的结论是( )
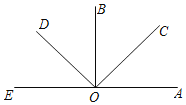
A.∠BOC=∠AOC=∠BOD
B.图中小于平角的角有6个
C.∠BOC与∠AOD互补
D.∠BOD和∠AOC互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=![]() 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).
(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=![]() 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com