【题目】为了解七年级学生身体发育状况，学校抽取一部分学生测量身高（单位：m），绘制处如下的统计图①和图②．请根据相关信息，解答下列问题：
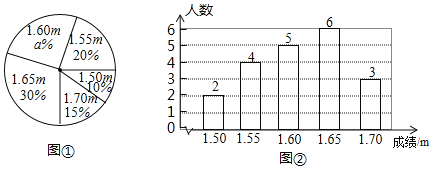
（1）图①中a的值为 ；
（2）求统计的这组学生身高数据的平均数、众数和中位数；
（3）如果全校七年级学生有300人，那么估计身高大于1.65m的学生大约有多少人？
【答案】（1）25；（2）平均数为1.61；众数是1.65；中位数是1.60；（3）135.
【解析】
（1）用整体1减去其它所占的百分比，即可求出a的值；
（2）根据平均数、众数和中位数的定义分别进行解答即可；
（3）根据高大于1.65m的学生所占的比例即可得到结果．
解：（1）根据题意得：1﹣20%﹣10%﹣15%﹣30%＝25%，
即a的值是25；
故答案为：25；
（2）观察条形统计图得：身高数据的平均数＝
＝1.61；
∵在这组数据中，1.65出现了6次，出现的次数最多，
∴这组数据的众数是1.65；
将这组数据从小到大排列，其中处于中间的两个数都是1.60，
则这组数据的中位数是1.60；
（3）全校七年级学生身高大于1.65m的学生大约有300×
＝135（人）．
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知抛物线
.
(1)求抛物线的对称轴(用含
的式子去表示)；
(2)若点
，
，
都在抛物线上，则
、
、
的大小关系为_______；
(3)直线
与
轴交于点
，与
轴交于点
，过点作垂直于轴的直线
与抛物线有两个交点，在抛物线对称轴右侧的点记为
，当
为钝角三角形时，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2018年9月17日世界人工智能大会在．上海召开，人工智能的变革力在教育、制造等领域加速落地．在某市举办的一次中学生机器人足球赛中，有四个代表队进入决赛，决赛中，每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛)，以下是积分表的一-部分．
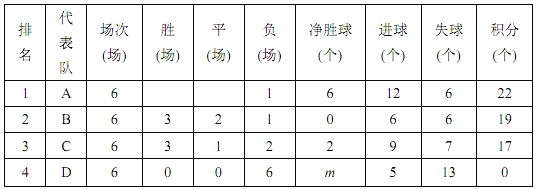
(说明：积分=胜场积分十平场积分+负场积分)
（1）D代表队的净胜球数m=______；
（2）本次决赛中，胜一场积______分，平一场积______分，负一场积_______分；
（3）此次竞赛的奖金分配方案为：进入决赛的每支代表队都可以获得参赛奖金6000元；另外，在决赛期间，每胜一场可以再获得奖金2000元，每平一场再获得奖金1000元．请根据表格提供的信息，求出冠军A队一共能获得多少奖金．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠CAB＝90°，AB＝AC，点A在y轴上，BC∥x轴，点B
．将△ABC绕点A顺时针旋转的△AB′C′，当点B′落在x轴的正半轴上时，点C′的坐标为（ ）
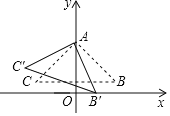
A.（﹣
，
﹣1）B.（﹣，﹣1）
C.（﹣，+1）D.（﹣，﹣1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）（问题发现）
如图1，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，延长CA到点F，使得AF＝AC，连接DF、BE，则线段BE与DF的数量关系为 ，位置关系为 ；
（2）（拓展研究）
将△ADE绕点A旋转，（1）中的结论有无变化？仅就图（2）的情形给出证明；
（3）（解决问题）
当AB＝2，AD＝
，△ADE旋转得到D，E，F三点共线时，直接写出线段DF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题提出
（1）如图①，在矩形ABCD中，AB=2AD，E为CD的中点，则∠AEB ∠ACB（填“＞”“＜”“=”）；
问题探究
（2）如图②，在正方形ABCD中，P为CD边上的一个动点，当点P位于何处时，∠APB最大？并说明理由；
问题解决
（3）如图③，在一幢大楼AD上装有一块矩形广告牌，其侧面上、下边沿相距6米（即AB=6米），下边沿到地面的距离BD=11.6米．如果小刚的睛睛距离地面的高度EF为1.6米，他从远处正对广告牌走近时，在P处看广告效果最好（视角最大），请你在图③中找到点P的位置，并计算此时小刚与大楼AD之间的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
