
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№ЯрНЛгк
жсЗжБ№ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌХзЮяЯп
СНЕуЃЌХзЮяЯп![]()
![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌНЛ
ЃЌНЛ![]() жсе§АыжсгкЕу
жсе§АыжсгкЕу![]() ЃЎ
ЃЎ
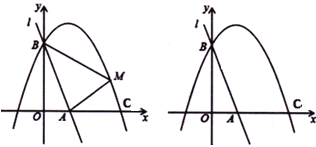
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу![]() дкЕквЛЯѓЯоФкЃЌСЌНг
дкЕквЛЯѓЯоФкЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГі
ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГі![]() ЕФзюДѓжЕМАДЫЪБЖЏЕу
ЕФзюДѓжЕМАДЫЪБЖЏЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉНЋЕу![]() ШЦдЕуа§зЊЕУЕу
ШЦдЕуа§зЊЕУЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌдка§зЊЙ§ГЬжаЃЌвЛЖЏЕу
ЃЌдка§зЊЙ§ГЬжаЃЌвЛЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЯпЖЮ
ГіЗЂЃЌбиЯпЖЮ![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛЕФЫйЖШдЫЖЏЕН
ИіЕЅЮЛЕФЫйЖШдЫЖЏЕН![]() ЃЌдйбиЯпЖЮ
ЃЌдйбиЯпЖЮ![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЕН
ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЕН![]() КѓЭЃжЙЃЌЧѓЕу
КѓЭЃжЙЃЌЧѓЕу![]() дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧЖрЩйЃП
дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЕФзюДѓжЕЪЧ
ЕФзюДѓжЕЪЧ![]() ЃЌДЫЪБЖЏЕу
ЃЌДЫЪБЖЏЕу![]() ЕФзјБъЪЧ
ЕФзјБъЪЧ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() УыЃЎ
УыЃЎ
ЁОНтЮіЁП
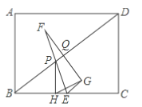
ЃЈ1ЃЉИљОнжБЯпlЕФНтЮіЪНПЩЧѓГіЕуBзјБъЃЌАбЕуBзјБъДњШы![]() ПЩЧѓГіaжЕЃЌМДПЩЕУХзЮяЯпНтЮіЪНЃЛ
ПЩЧѓГіaжЕЃЌМДПЩЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌСЌНгOMЃЌЙ§ЕуMзїMEЁЭyжсгкEЃЌMDЁЭxжсгкDЃЌИљОнЃЈ1ЃЉжаЫљЧѓХзЮяЯпНтЮіЪНПЩЧѓГіЕуCзјБъЃЌПЩЕУГіmЕФШЁжЕЗЖЮЇЃЌИљОнжБЯпlНтЮіЪНПЩЧѓГіAЕузјБъЃЌИљОн![]() МДПЩЕУSЙигкmЕФЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓГіSЕФзюДѓжЕКЭЕуMЕФзјБъЃЛ
МДПЩЕУSЙигкmЕФЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓГіSЕФзюДѓжЕКЭЕуMЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌИљОнЬтвтзїЕуHЃЈ0ЃЌ![]() ЃЉЃЌСЌНгHAЁфЁЂOAЁфЁЂBAЁфЁЂCAЁфЃЌПЩжЄУї
ЃЉЃЌСЌНгHAЁфЁЂOAЁфЁЂBAЁфЁЂCAЁфЃЌПЩжЄУї![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌРћгУЙДЙЩЖЈРэЧѓГіHCЕФГЄМДПЩЕУЕу
ЃЌРћгУЙДЙЩЖЈРэЧѓГіHCЕФГЄМДПЩЕУЕу![]() дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЕФЪБМфЃЎ
дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЕФЪБМфЃЎ
ЃЈ1ЃЉНЋ![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЁпХзЮяЯп![]()
![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМЃЌСЌНгOMЃЌЙ§ЕуMзїMEЁЭyжсгкEЃЌMDЁЭxжсгкDЃЌ
НЋ![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЁпЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕу![]() дквЛЯѓЯоФкЃЌЕу
дквЛЯѓЯоФкЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
НЋ![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъ
ЕФзјБъ![]() ЃЌ
ЃЌ
Ёр![]()
![]()
=![]() OBЁЄME+
OBЁЄME+![]() OAЁЄMD-
OAЁЄMD-![]() OBЁЄOA
OBЁЄOA
![]() ЃЌ
ЃЌ
ЛЏМђЕУЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ-m2+2m+3=
ЪБЃЌ-m2+2m+3=![]() ЃЌ
ЃЌ
Ёр![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌ
ШЁЕУзюДѓжЕЃЌ![]() ЕФзюДѓжЕЪЧ
ЕФзюДѓжЕЪЧ![]() ЃЌДЫЪБЖЏЕу
ЃЌДЫЪБЖЏЕу![]() ЕФзјБъЪЧ
ЕФзјБъЪЧ![]() ЃЎ
ЃЎ
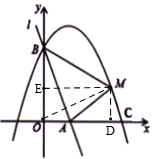
ЃЈ3ЃЉШчЭМЃЌШЁЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁпЕуPдкBAЁфЩЯдЫЖЏЕФЫйЖШЪЧУПУы3ИіЕЅЮЛГЄЖШЃЌдкCAЁфЩЯдЫЖЏЕФЫйЖШЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌ
ЁрдкBAЁфЩЯдЫЖЏЕФЪБМфЮЊ![]() ЃЌдкCAЁфЩЯдЫЖЏЕФЪБМфЮЊAЁфCЃЌ
ЃЌдкCAЁфЩЯдЫЖЏЕФЪБМфЮЊAЁфCЃЌ
Ёп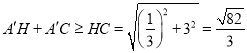 ЃЌ
ЃЌ
ЁрЕу![]() дкећИідЫЖЏЙ§ГЬжагУЪБ
дкећИідЫЖЏЙ§ГЬжагУЪБ![]() ЃЌМДЕу
ЃЌМДЕу![]() дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧ
дкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЪЧ![]() УыЃЎ
УыЃЎ
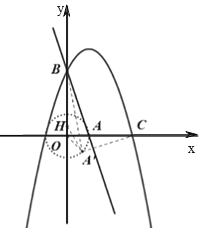


 ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ
ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЮЊЖдНЧЯп
ЮЊЖдНЧЯп![]() ЩЯЕФЖЏЕуЃЌЩш
ЩЯЕФЖЏЕуЃЌЩш![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ВЂбгГЄжСЕу
ВЂбгГЄжСЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌзїЕу
ЃЌзїЕу![]() Йигк
Йигк![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБЕу![]() дЫЖЏЕНЖдНЧЯп
дЫЖЏЕНЖдНЧЯп![]() ЕФжаЕуЪБЃЌЧѓ
ЕФжаЕуЪБЃЌЧѓ![]() ЕФжмГЄЃЛ
ЕФжмГЄЃЛ
ЃЈ3ЃЉдкЕу![]() ЕФдЫЖЏЕФЙ§ГЬжаЃЌ
ЕФдЫЖЏЕФЙ§ГЬжаЃЌ![]() ЪЧЗёПЩвдЮЊЕШбќШ§НЧаЮЃПШєПЩвдЃЌЧѓГі
ЪЧЗёПЩвдЮЊЕШбќШ§НЧаЮЃПШєПЩвдЃЌЧѓГі![]() ЕФжЕЃЛШєВЛПЩвдЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛПЩвдЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ
ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§![]() Еузї
Еузї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]()
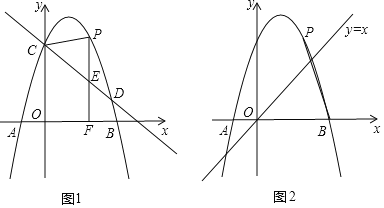
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН
ЃЈ2ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЗНЃЌЧв
ЩЯЗНЃЌЧв![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ
ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕФзјБъ
ЕФзјБъ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌШєЕу![]() ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊжБНЧЖЅЕуЃЌЯпЖЮ
ЮЊжБНЧЖЅЕуЃЌЯпЖЮ![]() ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ
ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ![]() ЕФ
ЕФ![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЧЁКУТфдкжБЯп
ЧЁКУТфдкжБЯп![]() ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу
ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу![]() ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
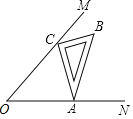
ЁОЬтФПЁПШчЭМЃЌЁЯMONЃН45ЁуЃЌвЛжБНЧШ§НЧГпЁїABCЕФСНИіЖЅЕуCЁЂAЗжБ№дкOMЃЌONЩЯвЦЖЏЃЌШєACЃН6ЃЌдђЕуOЕНACОрРыЕФзюДѓжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪ§бЇЛюЖЏаЁзщдквЛДЮЛюЖЏжаЃЌЖдвЛИіЪ§бЇЮЪЬтзїШчЯТЬНОПЃК
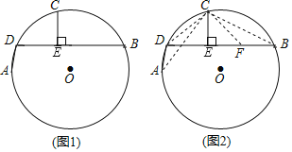
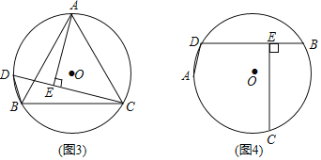
ЃЈЮЪЬтЗЂЯжЃЉШчЭМ1ЃЌADЃЌBDЮЊЁбOЕФСНЬѕЯвЃЈADЃМBDЃЉЃЌЕуCЮЊ![]() ЕФжаЕуЃЌЙ§CзїCEЁЭBDЃЌДЙзуЮЊEЃЎЧѓжЄЃКBEЃНDE+ADЃЎ
ЕФжаЕуЃЌЙ§CзїCEЁЭBDЃЌДЙзуЮЊEЃЎЧѓжЄЃКBEЃНDE+ADЃЎ
ЃЈЮЪЬтЬНОПЃЉаЁУїЭЌбЇЕФЫМТЗЪЧЃКШчЭМ2ЃЌдкBEЩЯНиШЁBFЃНADЃЌСЌНгCAЃЌCBЃЌCDЃЌCFЃЎЁЁЧыФуАДееаЁУїЕФЫМТЗЭъГЩЩЯЪіЮЪЬтЕФжЄУїЙ§ГЬЃЎ
ЃЈНсТлдЫгУЃЉШчЭМ3ЃЌЁїABCЪЧЁбOЕФФкНгЕШБпШ§НЧаЮЃЌЕуDЪЧ![]() ЩЯвЛЕуЃЌЁЯACDЃН45ЁуЃЌСЌНгBDЃЌCDЃЌЙ§ЕуAзїAEЁЭCDЃЌДЙзуЮЊEЃЎШєABЃН
ЩЯвЛЕуЃЌЁЯACDЃН45ЁуЃЌСЌНгBDЃЌCDЃЌЙ§ЕуAзїAEЁЭCDЃЌДЙзуЮЊEЃЎШєABЃН![]() ЃЌдђЁїBCDЕФжмГЄЮЊЁЁ ЁЁЃЎ
ЃЌдђЁїBCDЕФжмГЄЮЊЁЁ ЁЁЃЎ
ЃЈБфЪНЬНОПЃЉШчЭМ4ЃЌШєНЋЃЈЮЪЬтЗЂЯжЃЉжаЁАЕуCЮЊ![]() ЕФжаЕуЁБИФЮЊЁАЕуCЮЊгХЛЁ
ЕФжаЕуЁБИФЮЊЁАЕуCЮЊгХЛЁ![]() ЕФжаЕуЁБЃЌЦфЫћЬѕМўВЛБфЃЌЩЯЪіНсТлЁАBEЃНDE+ADЁБЛЙГЩСЂТ№ЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧыаДГіBEЁЂADЁЂDEжЎМфЕФаТЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЕФжаЕуЁБЃЌЦфЫћЬѕМўВЛБфЃЌЩЯЪіНсТлЁАBEЃНDE+ADЁБЛЙГЩСЂТ№ЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧыаДГіBEЁЂADЁЂDEжЎМфЕФаТЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018Фъ9дТ17ШеЪРНчШЫЙЄжЧФмДѓЛсдкЃЎЩЯКЃейПЊЃЌШЫЙЄжЧФмЕФБфИяСІдкНЬг§ЁЂжЦдьЕШСьгђМгЫйТфЕиЃЎдкФГЪаОйАьЕФвЛДЮжабЇЩњЛњЦїШЫзуЧђШќжаЃЌгаЫФИіДњБэЖгНјШыОіШќЃЌОіШќжаЃЌУПИіЖгЗжБ№гыЦфЫќШ§ИіЖгНјаажїПЭГЁБШШќИївЛГЁ(МДУПИіЖгвЊНјаа6ГЁБШШќ)ЃЌвдЯТЪЧЛ§ЗжБэЕФвЛ-ВПЗжЃЎ
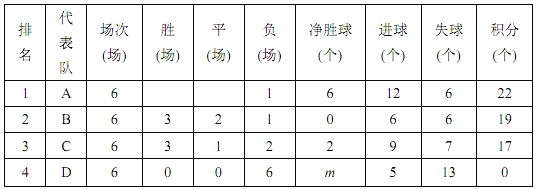
(ЫЕУїЃКЛ§Зж=ЪЄГЁЛ§ЗжЪЎЦНГЁЛ§Зж+ИКГЁЛ§Зж)
ЃЈ1ЃЉDДњБэЖгЕФОЛЪЄЧђЪ§m=______ЃЛ
ЃЈ2ЃЉБОДЮОіШќжаЃЌЪЄвЛГЁЛ§______ЗжЃЌЦНвЛГЁЛ§______ЗжЃЌИКвЛГЁЛ§_______ЗжЃЛ
ЃЈ3ЃЉДЫДЮОКШќЕФНБН№ЗжХфЗНАИЮЊЃКНјШыОіШќЕФУПжЇДњБэЖгЖМПЩвдЛёЕУВЮШќНБН№6000дЊЃЛСэЭтЃЌдкОіШќЦкМфЃЌУПЪЄвЛГЁПЩвддйЛёЕУНБН№2000дЊЃЌУПЦНвЛГЁдйЛёЕУНБН№1000дЊЃЎЧыИљОнБэИёЬсЙЉЕФаХЯЂЃЌЧѓГіЙкОќAЖгвЛЙВФмЛёЕУЖрЩйНБН№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
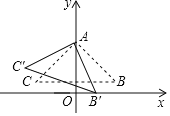
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCABЃН90ЁуЃЌABЃНACЃЌЕуAдкyжсЩЯЃЌBCЁЮxжсЃЌЕуB![]() ЃЎНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕФЁїABЁфCЁфЃЌЕБЕуBЁфТфдкxжсЕФе§АыжсЩЯЪБЃЌЕуCЁфЕФзјБъЮЊЃЈЁЁЁЁЃЉ
ЃЎНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕФЁїABЁфCЁфЃЌЕБЕуBЁфТфдкxжсЕФе§АыжсЩЯЪБЃЌЕуCЁфЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉB.ЃЈЉ
Љ1ЃЉB.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉ
Љ1ЃЉ
C.ЃЈЉ![]() ЃЌ
ЃЌ![]() +1ЃЉD.ЃЈЉ
+1ЃЉD.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉ
Љ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
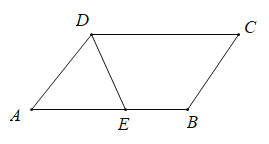
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЕФЦНЗжЯпгыБп
ЕФЦНЗжЯпгыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЕу![]() гыЕу
гыЕу![]() жиКЯЃЌЧыжБНгаДГіЫФБпаЮ
жиКЯЃЌЧыжБНгаДГіЫФБпаЮ![]() ЪЧФФжжЬиЪтЕФЦНааЫФБпаЮЃЎ
ЪЧФФжжЬиЪтЕФЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаФтгкжаЧяНкЧА![]() ЬьРяЯњЪлФГЦЗХЦдТБ§ЃЌЦфНјМлЮЊ
ЬьРяЯњЪлФГЦЗХЦдТБ§ЃЌЦфНјМлЮЊ![]() дЊ/
дЊ/![]() ЃЎЩшЕк
ЃЎЩшЕк![]() ЬьЕФЯњЪлМлИёЮЊ
ЬьЕФЯњЪлМлИёЮЊ![]() (дЊ/
(дЊ/![]() )ЯњЪлСПЮЊ
)ЯњЪлСПЮЊ![]() ЃЎИУГЌЪаИљОнвдЭљЕФЯњЪлОбщЕУГівдЯТЕФЯњЪлЙцТЩЃКЂйгы
ЃЎИУГЌЪаИљОнвдЭљЕФЯњЪлОбщЕУГівдЯТЕФЯњЪлЙцТЩЃКЂйгы![]() ТњзувЛДЮКЏЪ§ЙиЯЕЃЌЧвЕБ
ТњзувЛДЮКЏЪ§ЙиЯЕЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎЂк
ЃЎЂк![]() гы
гы![]() ЕФЙиЯЕЮЊ
ЕФЙиЯЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉ![]() гы
гы![]() ЕФЙиЯЕЪНЮЊ________ЃЛ
ЕФЙиЯЕЪНЮЊ________ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓЕкМИЬьЕФЯњЪлРћШѓ
ЪБЃЌЧѓЕкМИЬьЕФЯњЪлРћШѓ![]() (дЊ)зюДѓЃПзюДѓРћШѓЮЊЖрЩйЃП
(дЊ)зюДѓЃПзюДѓРћШѓЮЊЖрЩйЃП
ЃЈ3ЃЉШєдкЕБЬьЯњЪлМлИёЕФЛљДЁЩЯеЧ![]() дЊ/
дЊ/![]() ЃЌдкЕк
ЃЌдкЕк![]() ЬьжС
ЬьжС![]() ЬьЯњЪлРћШѓзюДѓжЕЮЊ
ЬьЯњЪлРћШѓзюДѓжЕЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com