
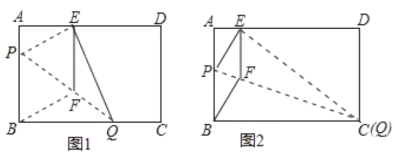
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() 也随之移动;
也随之移动;
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() 分别在边
分别在边![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
【答案】(1)见解析;(2)①![]() ,②
,②![]()
【解析】
(1)根据轴对称的性质得到![]() ,
,![]() ,
,![]() ,再由平行线的性质得到
,再由平行线的性质得到![]() ,从而得到
,从而得到![]() ,由“等角对等边”得到EP=EF,进而得出
,由“等角对等边”得到EP=EF,进而得出![]() 即可;
即可;
(2)①先由折叠得:EC=BC=10,利用勾股定理得:ED=8,设PE=x,则PB=x,AP=6x,Rt△APE中,由勾股定理得:(6x)2+22=x2,解出即可;
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=2cm;当点P与点A重合时,点E离点A最远,AE=AB=6cm,即可得出答案;
解:(1)证明:![]() 折叠纸片使
折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,
,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为菱形;
为菱形;
(2)解:①![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,点C与点Q重合,
对称,点C与点Q重合,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ;
;
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 菱形
菱形![]() 的边长为
的边长为![]() ;
;
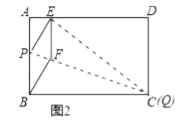
②当点![]() 与点
与点![]() 重合时,如图2;
重合时,如图2;
点![]() 离点
离点![]() 最近,由①知,此时
最近,由①知,此时![]() ;
;
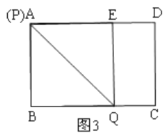
当点![]() 与点
与点![]() 重合时,如图3所示:
重合时,如图3所示:
点![]() 离点
离点![]() 最远,此时四边形
最远,此时四边形![]() 为正方形,
为正方形,![]() ,
,
![]() 点
点![]() 在边
在边![]() 上移动的最大距离为6-2=
上移动的最大距离为6-2=![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
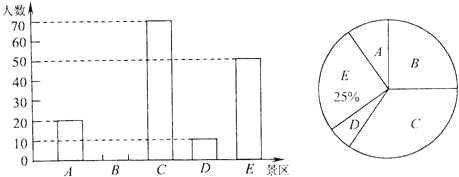
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为( )
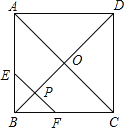
A. 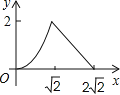 B.
B. 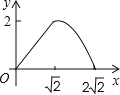
C. 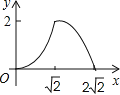 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
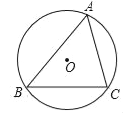
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
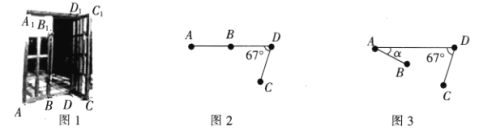
(1)求点C到AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com