
【题目】如图,抛物线![]() 交x轴于A、B两点(点A在点B的左侧),
交x轴于A、B两点(点A在点B的左侧),![]() .
.
(1)求抛物线的函数表达式;
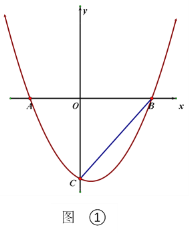
(2)如图①,连接BC,点P在抛物线上,且∠BCO=![]() ∠PBA.求点P的坐标
∠PBA.求点P的坐标
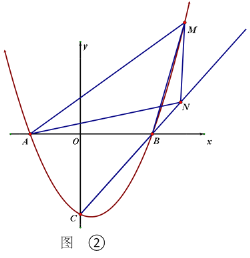
(3)如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,![]() ,点M到
,点M到![]() 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)![]() ;(2)P
;(2)P ![]() 或
或![]() ;(3)MN的为定值,定值为5
;(3)MN的为定值,定值为5
【解析】
(1)由函数解析式![]() 可确定A(
可确定A(![]() ,0),B
,0),B![]() ,再由
,再由![]() ;列出关于
;列出关于![]() 的方程即可求解;
的方程即可求解;
(2)作线段BC的垂直平分线交![]() 轴于点D,此时DC=DB,构造∠ODB=2∠BCO=∠PBA,将∠BCO=
轴于点D,此时DC=DB,构造∠ODB=2∠BCO=∠PBA,将∠BCO=![]() ∠PBA条件转化为
∠PBA条件转化为![]() ,然后设P
,然后设P![]() ,根据
,根据![]() 列方程求解即可;
列方程求解即可;
(3)由已知可求得![]() ,从而可得
,从而可得![]() ,进而可得点B、N到直线AM的距离相等,所以
,进而可得点B、N到直线AM的距离相等,所以![]() ∥BN,再证明
∥BN,再证明![]() (ASA)即可得到MN=AB=5.
(ASA)即可得到MN=AB=5.
解:(1)把![]() 代入抛物线
代入抛物线![]() ,得
,得![]() 或
或![]() ,
,
∵点A在点B的左侧,
∴A(![]() ,0),B
,0),B![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线的函数表达式为:![]() ;
;
(2)如图③,作线段BC的垂直平分线交![]() 轴于点D,此时DC=DB,
轴于点D,此时DC=DB,
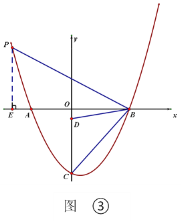
∵DC=DB,
∴∠DCB=∠DBC,
∴∠ODB=∠DCB+∠DBC=2∠BCO,
∵∠BCO=![]() ∠PBA,
∠PBA,
∴∠PBA=2∠BCO,
∴∠ODB=∠PBA,
∴![]() ,
,
设P![]() ,DC=DB=
,DC=DB=![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,

在![]() 中,
中,![]() 解得
解得![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,即
,即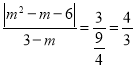 ,解得
,解得![]() ,
,
∴![]() 或
或![]() ,
,
∴点P的坐标为![]() 或
或![]() ;
;
(3)MN的为定值,定值为5;
∵![]() ,点M到
,点M到![]() 轴的距离为2L,
轴的距离为2L,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 和
和![]() 有同底AM,
有同底AM,
∴点B、N到直线AM的距离相等,
∴![]() ∥BN,
∥BN,
∴∠MAN=∠ANB,∠AMB=∠MBN,∠ABC=∠MAB,
∵∠ANB=∠MBN,
∴∠MAN=∠AMB,
∵![]() =
=![]() =
=![]() =2,
=2,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,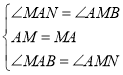 ,
,
∴![]() (ASA),
(ASA),
∴MN=AB=5,
∴MN的为定值,定值为5.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
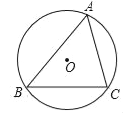
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
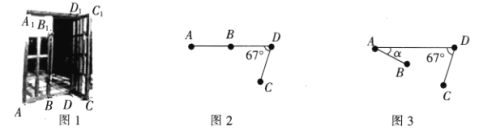
(1)求点C到AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△AOB,点C是边AO所在直线上的动点,点D是x轴上的动点,在矩形CDEF中,CD=6,DE=![]() ,则OF的最小值为___________.
,则OF的最小值为___________.
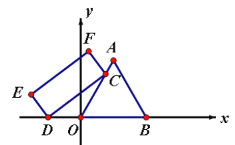
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“壮丽70载,奋进新时代”.值伟大祖国70华诞之际,某网店特别推出甲、乙两种纪念文化衫,已知甲种纪念文化衫的售价比乙种纪念文化衫多15元,广益中学陈老师从该网店购买了2件甲种纪念文化衫和3件乙种纪念文化衫,共花费255元.
(1)该网店甲、乙两种纪念文化衫每件的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种纪念文化衫共200件,且甲种纪念文化衫的数量大于乙种纪念文化衫数量的![]() ,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
①若设购进甲种纪念文化衫m件,则该网店有哪几种进货方案?
②若所购进纪念文化衫均可全部售出,请求出网店所获利润W(元)与甲种纪念文化衫进货量m(件)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三点![]() ,
,![]() ,
,![]() ,其中有两点同时在反比例函数
,其中有两点同时在反比例函数![]() 的图象上.将这两点分别记为
的图象上.将这两点分别记为![]() ,另一点记为
,另一点记为![]() .
.
(1)求出![]() 的值;
的值;
(2)求直线![]() 对应的一次函数的表达式.
对应的一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,学校决定围绕“音乐、体育、美术、书法、其它活动项目中,你参加哪一项活动(每人只限一项)的问题”,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:

(1)在这次调查中一共抽查了多少名学生?
(2)求参加“音乐”活动项目的人数占抽查总人数的百分比.
(3)若全校有2400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com