练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

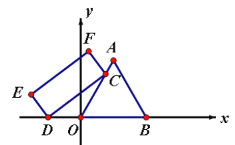
    【题目】如图，等边△AOB，点C是边AO所在直线上的动点，点D是x轴上的动点，在矩形CDEF中，CD=6，DE=，则OF的最小值为___________．

    【答案】

    【解析】

    由已知可知∠COD=120°，CD=6，根据定弦定角是圆，找到 △COD的外接圆圆心G位于EF的中点，即可利用点到圆上的距离最小值解决题．

    解：取EF的中点G，连接DG、CD、OG，并以DG为半径以G为圆心作圆，

    ∵在矩形CDEF中，CD=6，DE=，

    ∴EG=FG=3，

    ∴tan∠EGD=

    ∴∠EGD=30°，DG=CG=,

    ∴∠CGD=120°，

    ∵在等边△AOB中∠AOB=60°，

    ∴∠AOD=120°，

    ∴，

    ∴C、D、O和圆G上任意一点共圆，即点O在上，

    ∴DG=OG=，

    在△FGO中，，

    ∴，

    ∴OF的最小值为．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若函数是关于的反比例函数。

    （1）求的值；

    （2）函数图象在哪些象限？在每个象限内，随的增大而怎样变化？

    （3）当时，求的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司投入研发费用40万元(40万元只计入第一年成本)，成功研发出一种产品．公司按订单生产(产量＝销售量)，第一年该产品正式投产后，生产成本为4元/件．此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y＝﹣x+20．

    (1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式；

    (2)该产品第一年的利润为24万元，那么该产品第一年的售价是多少？

    (3)第二年，该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发，使产品的生产成本降为3元/件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过10万件．请计算该公司第二年的利润W2至少为多少万元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】诗词是中华民族灿烂文化中的瑰宝，王老师连续三个月在班上开展针对全班同学的古诗词默写的测试活动．如图，王老师将三次默写的成绩（满分10分）做了统计，并绘制了折线统计图．由图可知，以下结论错误的是（ ）

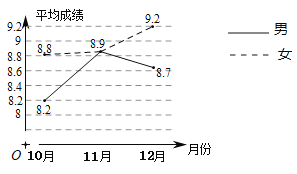
    A.男、女生11月份的平均成绩相同

    B.10月到12月，女生的平均成绩一直在进步

    C.10月到11月，女生的平均成绩的增长率约为8.5%

    D.11月到12月女生的平均成绩比10月到11月的增长快

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=﹣x2+bx+c与x轴交于点A(﹣1，0)和点B(3，0)．P为该抛物线上一动点，设点P的横坐标为m．

    （1）求抛物线的解析式．

    （2）将该抛物线沿y轴向下平移AB个单位长度，点P的对应点为P′，若OP=OP′，求△OP P′的面积．

    （3）如图2，连接AP，BP，设△APB的面积为S，当-2≤m≤2时，直接写出S的最大值．

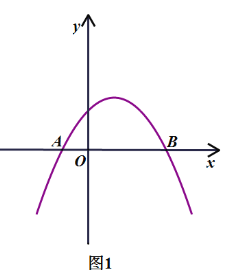
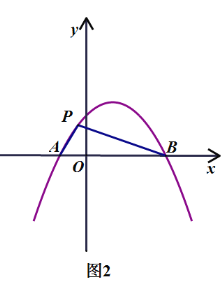
    查看答案和解析>>

    科目：初中数学 来源： 题型：

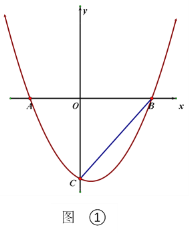
    【题目】如图，抛物线交x轴于A、B两点（点A在点B的左侧），．

    （1）求抛物线的函数表达式；

    （2）如图①，连接BC，点P在抛物线上，且∠BCO=∠PBA．求点P的坐标

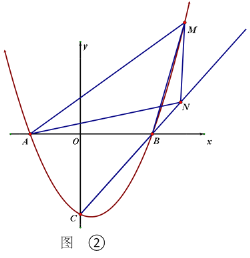
    （3）如图②，M是抛物线上一点，N为射线CB上的一点，且M、N两点均在第一象限内，B、N是位于直线AM同侧的不同两点，，点M到轴的距离为2L，△AMN的面积为5L，且∠ANB=∠MBN，请问MN的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF．，GH．

    （1）填空：∠AHC　 　∠ACG；（填“＞”或“＜”或“＝”）

    （2）线段AC，AG，AH什么关系？请说明理由；

    （3）设AE＝m，

    ①△AGH的面积S有变化吗？如果变化．请求出S与m的函数关系式；如果不变化，请求出定值．

    ②请直接写出使△CGH是等腰三角形的m值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

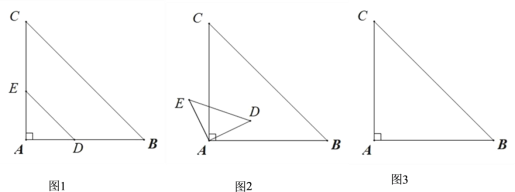
    【题目】如图 1，在等腰直角△ABC 中，∠A =90°，AB=AC=3，在边 AB 上取一点 D（点 D 不与点 A，B 重合），在边 AC 上取一点 E，使 AE=AD，连接 DE. 把△ADE 绕点 A 逆时针方向旋转α（0°＜α＜360°），如图 2．

    （1）请你在图 2 中，连接 CE 和 BD，判断线段 CE 和 BD 的数量关系，并说明理由；

    （2）请你在图 3 中，画出当α =45°时的图形，连接 CE 和 BE，求出此时△CBE 的面积；

    （3）若 AD=1，点 M 是 CD 的中点，在△ADE 绕点 A 逆时针方向旋转的过程中，线段AM 的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形OABC的一个顶点B的坐标是（4，2），反比例函数y=（x＞0）的图象经过矩形的对称中点E，且与边BC交于点D，若过点D的直线y=mx+n将矩形OABC的面积分成3：5的两部分，则此直线的解析式为_____．

    查看答案和解析>>

    同步练习册答案