
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�ECF��45�㣬CF���ӳ��߽�BA���ӳ����ڵ�G��CE���ӳ��߽�DA���ӳ����ڵ�H������AC��EF����GH��
��1����գ���AHC�� ����ACG�������������������
��2���߶�AC��AG��AHʲô��ϵ����˵�����ɣ�
��3����AE��m��
�١�AGH�����S�б仯������仯�������S��m�ĺ�����ϵʽ��������仯���������ֵ��
����ֱ��д��ʹ��CGH�ǵ��������ε�mֵ��

���𰸡���1��=����2�����ۣ�AC2��AGAH�����ɼ���������3���١�AGH��������䣮��m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��.
��.
��������
��1��֤����DAC=��AHC+��ACH=45�㣬��ACH+��ACG=45���������Ƴ���AHC=��ACG��
��2�����ۣ�AC2=AGAH��ֻҪ֤����AHC�ס�ACG���ɽ�����⣻
��3���١�AGH��������䣮���������ε������ʽ���㼴�ɣ�
�ڷ��������ηֱ���⼴�ɽ������.
��1�����ı���ABCD�������Σ�
��AB��CB��CD��DA��4����D����DAB��90����DAC����BAC��45�㣬
��AC��![]() ��
��
�ߡ�DAC����AHC+��ACH��45�㣬��ACH+��ACG��45�㣬
���AHC����ACG��
�ʴ�Ϊ����
��2�����ۣ�AC2��AGAH��
���ɣ��ߡ�AHC����ACG����CAH����CAG��135�㣬
���AHC�ס�ACG��
��![]() ��
��
��AC2��AGAH��
��3���١�AGH��������䣮
���ɣ���S��AGH��![]() AHAG��
AHAG��![]() AC2��
AC2��![]() ����4
����4![]() ��2��16��
��2��16��
���AGH�����Ϊ16��
����ͼ1�У���GC��GHʱ����֤��AHG�ա�BGC��
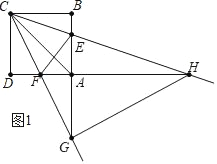
�ɵ�AG��BC��4��AH��BG��8��
��BC��AH��
��![]() ,
,
��AE��![]() AB��
AB��![]() ��
��
��ͼ2�У���CH��HGʱ��
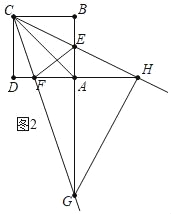
��֤AH��BC��4��
��BC��AH��
��![]() ��1��
��1��
��AE��BE��3��
��ͼ3�У���CG��CHʱ����֤��ECB����DCF��22.5��
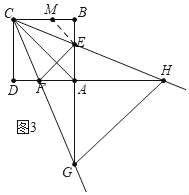
��BC��ȡһ��M��ʹ��BM��BE��
���BME����BEM��45�㣬
�ߡ�BME����MCE+��MEC��
���MCE����MEC��22.5�㣬
��CM��EM����BM��BE��m����CM��EM![]() m��
m��
��m+![]() m��6��
m��6��
��m��6��![]() ��1����
��1����
��AE��6��6��![]() ��1����12��6
��1����12��6![]() ��
��
��������������������m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڲ��ϸĽ�ѧϰ������С�Ϸ��֣��Խ�����лع˷�˼��ѧϰЧ�����ã�ijһ��С����20����ʱ�������ѧϰ������С�����ڽ����ʱ��![]() ����λ�����ӣ���ѧϰ������
����λ�����ӣ���ѧϰ������![]() �Ĺ�ϵ��ͼ1��ʾ�����ڻع˷�˼��ʱ��
�Ĺ�ϵ��ͼ1��ʾ�����ڻع˷�˼��ʱ��![]() ����λ�����ӣ���ѧϰ����
����λ�����ӣ���ѧϰ����![]() �Ĺ�ϵ��ͼ2��ʾ������
�Ĺ�ϵ��ͼ2��ʾ������![]() �������ߵ�һ���֣�
�������ߵ�һ���֣�![]() Ϊ�����ߵĶ��㣩�������ڻع˷�˼��ʱ�䲻�������ڽ����ʱ�䣮
Ϊ�����ߵĶ��㣩�������ڻع˷�˼��ʱ�䲻�������ڽ����ʱ�䣮
��1����С�Ͻ����ѧϰ������![]() �����ڽ����ʱ��
�����ڽ����ʱ��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����С�ϻع˷�˼��ѧϰ������![]() �����ڻع˷�˼��ʱ��
�����ڻع˷�˼��ʱ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����С����η������ͻع˷�˼��ʱ�䣬����ʹ��20���ӵ�ѧϰ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
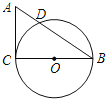
����Ŀ����Rt��ACB��,��C=90��,AC=3 cm,BC=4 cm,��BCΪֱ������O��AB�ڵ�D.
(1)���߶�AD�ij���;
(2)��E���߶�AC�ϵ�һ��,���ʵ���E��ʲôλ��ʱ,ֱ��ED�먑O����?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y1=(x��2)(x��4)��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����Գ���l��x�ύ�ڵ�C�����Ķ���Ϊ��D��
��1�����D������ ��
��2����P�ڶԳ���l�ϣ�λ�ڵ�C�Ϸ�����CP=2CD����PΪ����Ķ��κ���y2=ax2+bx+c��a��0����ͼ�����A��
����˵�����κ���y2=ax2+bx+c��a��0����ͼ�����B��
�ڵ�R�ڶ��κ���y1=��x��2����x��4����ͼ���ϣ���x��ľ���Ϊd������R������Ϊ ʱ�����κ���y2=ax2+bx+c��a��0����ͼ��������ֻ�������㵽x��ľ������2d��
����ͼ2����֪0��m��2������M��0��m����x���ƽ���ߣ��ֱ��κ���y1=��x��2����x��4��y2=ax2+bx+c��a��0����ͼ���ڵ�E��F��G��H����E��G�ڶԳ���l��ࣩ������H��x��Ĵ��ߣ�����Ϊ��N�������κ���y1=��x��2����x��4����ͼ���ڵ�Q������GHN�ס�EHQ����ʵ��m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
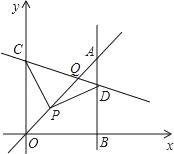
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪P��1��1����CΪy����������һ�㣬DΪ��һ������һ�㣬��PC��PD����CPD��90��������D��ֱ��AB��x����B��ֱ��AB��ֱ��y��x���ڵ�A����BD��3AD������CD��ֱ��CD��ֱ��y��x���ڵ�Q�����Q������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
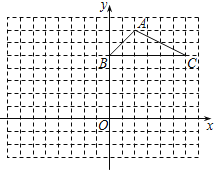
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�Ķ�
�㶼�ڸ���ϣ�����ƽ��ֱ������ϵ��
(1)��A������Ϊ ����C������Ϊ ��
(2)����ABC����ƽ��7����λ���뻭��ƽ�ƺ����A1B1C1����MΪ��ABC�ڵ�һ�㣬������Ϊ(a��b)����ƽ�ƺ��M�Ķ�Ӧ��M1������Ϊ ��
(3)��ԭ��OΪλ�����ģ�����ABC��С��ʹ�任��õ�����A2B2C2����ABC��Ӧ�ߵı�Ϊ1��2�����������ڻ�����A2B2C2����д����A2�����꣺ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
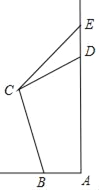
����Ŀ����ͼ����У������ʦ¥AD���С�������ѧ���ĸ��ֵ�չʾ��DE��ij��ѧ��ȤС���ͬѧ��������ѧ�����Ǻ���֪ʶ����ý�ʦ¥�ĸ߶ȣ����ڳ������ޣ��������������С�����¶�i��![]() ��1�Ľ��ݴӿ�̨ǰ��B��ǰ��50����C�������չʾ�Ƶײ�D������Ϊ45�㣬չʾ�ƶ���E������Ϊ53�㣨С�������ߺ��Բ��ƣ�����֪չʾ�Ƹ�DE��15�ף���ý�ʦ¥AD�ĸ߶�ԼΪ���������ף����ο����ݣ�Sin37���0��6��cos 37���0��8��tan37���0.75��
��1�Ľ��ݴӿ�̨ǰ��B��ǰ��50����C�������չʾ�Ƶײ�D������Ϊ45�㣬չʾ�ƶ���E������Ϊ53�㣨С�������ߺ��Բ��ƣ�����֪չʾ�Ƹ�DE��15�ף���ý�ʦ¥AD�ĸ߶�ԼΪ���������ף����ο����ݣ�Sin37���0��6��cos 37���0��8��tan37���0.75��![]() ��1.7��
��1.7��
A. 102.5B. 87.5C. 85D. 70
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
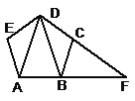
����Ŀ����ͼ���������ABCDE�У�DC��AB���ӳ��߽���F����ͼ�����DBF���Ƶ���������(���������������߶κ���ĸ����������DBF����) ( )
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������10�֣���ͼ��ֱ��y��x��m��������y��![]() ��bx��c��������A��1��0����
��bx��c��������A��1��0����
B��3��2����
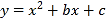
��1����m��ֵ�������ߵĽ���ʽ��
��2����ʽx2��bx��c��x��m�Ľ⼯����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com