
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�Ķ�
�㶼�ڸ���ϣ�����ƽ��ֱ������ϵ��
(1)��A������Ϊ ����C������Ϊ ��
(2)����ABC����ƽ��7����λ���뻭��ƽ�ƺ����A1B1C1����MΪ��ABC�ڵ�һ�㣬������Ϊ(a��b)����ƽ�ƺ��M�Ķ�Ӧ��M1������Ϊ ��
(3)��ԭ��OΪλ�����ģ�����ABC��С��ʹ�任��õ�����A2B2C2����ABC��Ӧ�ߵı�Ϊ1��2�����������ڻ�����A2B2C2����д����A2�����꣺ ��
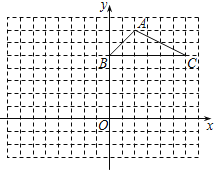
������ �⣺��1����2,8�� ��6,6����ͼ����2����![]() �� ��3��(
�� ��3��(![]() )
)
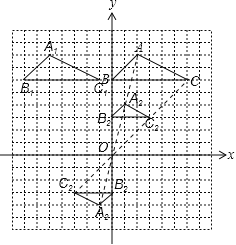
��������
��1��ֱ�Ӹ���ͼ�μ���д����A��C�����ꣻ
��2���ҳ�������ƽ�ƺ������Ķ�Ӧ�㣬Ȼ��˳�����Ӽ��ɣ�����ƽ�ƵĹ��ɼ���д����Mƽ�ƺ�����ꣻ
��3������λ�Ʊ任��Ҫ���ҳ��任��Ķ�Ӧ�㣬Ȼ��˳�����Ӹ��㼴�ɣ�ע�������������
�⣺��1��A������Ϊ����2��8����C������Ϊ����6��6����
��2������ͼ��������ʾ��������A1B1C1��Ϊ������ƽ�ƹ��ɣ���ƽ��7����λ����֪M1�����꣨a-7��b����
��3������ͼ��������ʾ��������A2B2C2��Ϊ����A2������Ϊ��1��4����-1��-4����


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���P������Ϊ(0��4)��ֱ��y��![]() x��3��x�ᡢy��ֱ��ڵ�A��B����M��ֱ��AB�ϵ�һ�����㣬��PM����СֵΪ________��
x��3��x�ᡢy��ֱ��ڵ�A��B����M��ֱ��AB�ϵ�һ�����㣬��PM����СֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB=8��CΪ��AB���е㣬PΪ��O��һ���㣬����AP��CP����C��CD��CP��AP�ڵ�D����P��B�˶���Cʱ�����D�˶���·����Ϊ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�Rt��ABC�У���ABC=90������CAB��ƽ���߽�BC�ڵ�O����OΪԲ�ģ�OB��Ϊ�뾶����O��
��1����֤����O��AC���У�
��2����AB=6��AC=10��
�����O�İ뾶��
����ͼ�ڣ��ӳ�AO����O�ڵ�D������D����O�����ߣ��ֱ�AC��AB���ӳ�����E��F������EF�ij���
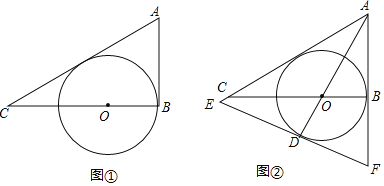
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�ECF��45�㣬CF���ӳ��߽�BA���ӳ����ڵ�G��CE���ӳ��߽�DA���ӳ����ڵ�H������AC��EF����GH��
��1����գ���AHC�� ����ACG�������������������
��2���߶�AC��AG��AHʲô��ϵ����˵�����ɣ�
��3����AE��m��
�١�AGH�����S�б仯������仯�������S��m�ĺ�����ϵʽ��������仯���������ֵ��
����ֱ��д��ʹ��CGH�ǵ��������ε�mֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD��һ��Ա�AD��BC���ӳ��߽��ڵ�E.
(1)��ͼ�٣�����ABC����ADC��90������֤��ED��EA��EC��EB��
(2)��ͼ�ڣ�����ABC��120����cos��ADC��![]() ��CD��5��AB��12����CDE�����Ϊ6�����ı���ABCD�������
��CD��5��AB��12����CDE�����Ϊ6�����ı���ABCD�������
(3)��ͼ�ۣ���һ��Ա�AB��DC���ӳ����ཻ�ڵ�F.��cos��ABC��cos��ADC��![]() ��CD��5��CF��ED��n��ֱ��д��AD�ij�(�ú�n��ʽ�ӱ�ʾ)��
��CD��5��CF��ED��n��ֱ��д��AD�ij�(�ú�n��ʽ�ӱ�ʾ)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ�ǡ�ABC�У�AB��BC����ABC��90�㣬BD��AC��D����M��AD�ϣ�����BM������C��CN��BM�ڵ�E����AB��N����BD��F������DE��AE��
��1������BCN��30�㣬EN��2����AN�ij���
��2����DE��AE��E��DG��DE��CN��G����֤��CE��![]() AE��
AE��
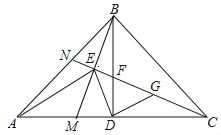
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���C=90�㣬AC=BC=2����һ�����dzߵ�ֱ�Ƕ�����б��AB���е�M�غϣ������dz����ŵ�M��תʱ����ֱ�DZ�ʼ�ձ��ֱַ����BC��AC����D��E����(D��E����B��A�غ�)��
(1)��֤��MD=ME��
(2)���ı���MDCE�������
(3)��ֻ��ԭ��Ŀ�еġ�AC=BC=2����Ϊ��BC=a��AC=b��(a��b)�����������䣬����̽����MD��ME�������?�����ȣ���֤�����������ȣ������MD��ME��ֵ��
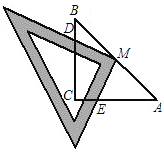
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��3��4���Ƿ���������![]() ͼ����һ�㣬������˵����ȷ���ǣ�������
ͼ����һ�㣬������˵����ȷ���ǣ�������
A. ͼ��ֱ�λ�ڶ���������B. �㣨2����6���ں���ͼ����
C. ��x��0ʱ��y��x���������СD. ��y��4ʱ��x��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com