
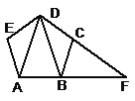
【题目】如图,已知:Rt△ABC中,∠C=90°,AC=BC=2,将一块三角尺的直角顶点与斜边AB的中点M重合,当三角尺绕着点M旋转时,两直角边始终保持分别与边BC、AC交于D,E两点(D、E不与B、A重合).
(1)求证:MD=ME;
(2)求四边形MDCE的面积:
(3)若只将原题目中的“AC=BC=2”改为“BC=a,AC=b,(a≠b)”其它都不变,请你探究:MD和ME还相等吗?如果相等,请证明;如果不相等,请求出MD∶ME的值.
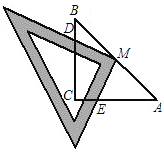
【答案】(1)证明见解析(2)1(3)不相等
【解析】
(1)证明MD和ME所在的△BDM≌△CEM即可;
(2)由(1)中的全等得到面积相等,把所求的四边形的面积进行转换,成为三角形的面积即可;
(3)过M点作MF⊥BC于F,MH⊥AC于H,证明△MFD![]() △MHE,再根据相似三角形的性质可得到MD∶ME的值.
△MHE,再根据相似三角形的性质可得到MD∶ME的值.
⑴、证明:连接CM,
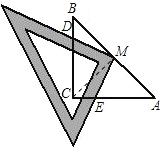
在Rt△ABC中,M是AB的中点,且AC=BC,
∴CM=![]() AB=BM
AB=BM
∠MCE=∠B=450,CM⊥AB
而∠BMD=900-∠DMC,∠EMC=900-∠DMC,
∴∠BMD=∠EMC
△BDM≌△CEM(ASA)
∴MD=ME
⑵、∵△BDM≌△CEM,∴S四边形DMEC=S△DMC+S△CME=S△DMC+S△BMD=S△BCM=![]() S△ACB=1,
S△ACB=1,
∴四边形MDCE的面积为1.
⑶、不相等.
如图所示,过M点作MF⊥BC于F,MH⊥AC于H,

∵M是AB的中点,
∴MF=![]() b,MH=
b,MH=![]() a
a
∠FMD=900-∠DMH,∠EMH=900-∠DMH,故∠FMD=∠EMH
∠MFD=∠MHE=900,
∴△MFD![]() △MHE,
△MHE,
∴![]() =
=![]() =
= ![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
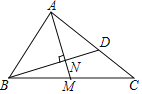
【题目】已知:如图,在△ABC中,∠BAC=90°,M是斜边BC的中点,BN⊥AM,垂足为点N,且BN的延长线交AC于点D.
(1)求证:△ABC∽△ADB;
(2)如果BC=20,BD=15,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
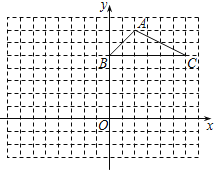
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶
点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 .
(2)将△ABC向左平移7个单位,请画出平移后的△A1B1C1.若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .
(3)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出△A2B2C2,并写出点A2的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |

成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE中,DC和AB的延长线交于F,则图中与△DBF相似的三角形有(不再添加其他的线段和字母,不包括△DBF本身) ( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农场有100棵果树,每一棵树平均结600个果子.现准备多种一些果树以提高产量,根据经验估计,每多种一棵果树,平均每棵树就会少结5个果子.假设果园增种x棵果树,果子总产量为y个.
(1)增种多少棵果树,可以使果园的总产量最多?最多为多少?
(2)增种多少棵果树,可以使果子的总产量在60400个以上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com