【题目】农场有100棵果树，每一棵树平均结600个果子．现准备多种一些果树以提高产量，根据经验估计，每多种一棵果树，平均每棵树就会少结5个果子．假设果园增种x棵果树，果子总产量为y个．
(1)增种多少棵果树，可以使果园的总产量最多？最多为多少？
(2)增种多少棵果树，可以使果子的总产量在60400个以上？
【答案】（1）当增种10棵果树时，可以使果园的总产量最多，最多为60500个（2）增种6、7、8、9、10、11、12、13、14棵果树，都可以使果子总产量在60400个以上
【解析】
（1）根据题意设增种x棵树，就可求出每棵树的产量，然后求出总产量y，再配方即可求解；
(2) 根据函数关系式y=-5x2+100x+60000=60400，结合一元二次方程解法得出即可．
(1)果园果子的总产量y=(100+x)(600－5x)= －5(x－10)2+60500，
故当增种10棵果树时，可以使果园的总产量最多，最多为60500个．
(2)由题意可知，当－5(x－10)2+60500=60400时，
，5.5<x<14.4.
∵抛物线对称轴为直线x=10，
∴增种6到14棵橙子树时，可以使果园橙子的总产量在60400个以上．
所以增种6、7、8、9、10、11、12、13、14棵果树，都可以使果子总产量在60400个以上
阅读快车系列答案科目：初中数学 来源： 题型：
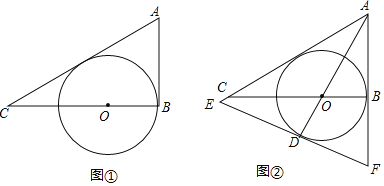
【题目】如图①，Rt△ABC中，∠ABC=90°，∠CAB的平分线交BC于点O，以O为圆心，OB长为半径作⊙O．
（1）求证：⊙O与AC相切．
（2）若AB=6，AC=10．
①求⊙O的半径；
②如图②，延长AO交⊙O于点D，过点D作⊙O的切线，分别交AC、AB的延长线于E、F，试求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
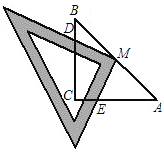
【题目】如图，已知：Rt△ABC中，∠C=90°，AC=BC=2，将一块三角尺的直角顶点与斜边AB的中点M重合，当三角尺绕着点M旋转时，两直角边始终保持分别与边BC、AC交于D，E两点(D、E不与B、A重合)．
(1)求证：MD=ME；
(2)求四边形MDCE的面积：
(3)若只将原题目中的“AC=BC=2”改为“BC=a，AC=b，(a≠b)”其它都不变，请你探究：MD和ME还相等吗?如果相等，请证明；如果不相等，请求出MD∶ME的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为
，到y轴的距离为
，若
，则称为点P的最大距离；若
，则称为点P的最大距离.
例如：点P（
，
）到到x轴的距离为4，到y轴的距离为3，因为3 < 4，所以点P的最大距离为.
（1）①点A（2，
）的最大距离为 ；
②若点B（
，
）的最大距离为
，则的值为 ；
（2）若点C在直线
上，且点C的最大距离为，求点C的坐标；
（3）若⊙O上存在点M，使点M的最大距离为，直接写出⊙O的半径r的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y＝ax2＋bx＋c(a≠0)的部分图象，其顶点坐标为(1，n)，抛物线与x轴的一个交点在点(3，0)和(4，0)之间．则下列结论
①a－b＋c＞0；②3a＋b＝0；
③b2＝4a(c－n)；
④一元二次方程ax2＋bx＋c＝n－1有两个不相等的实数根．
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若点A（3，4）是反比例函数
图象上一点，则下列说法正确的是（ ）
A. 图象分别位于二、四象限B. 点（2，﹣6）在函数图象上
C. 当x＜0时，y随x的增大而减小D. 当y≤4时，x≥3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P在直线y=x-1上，设过点P的直线交抛物线y=x2于A(a，a2)，B(b，b2)两点，当满足PA=PB时，称点P为“优点”.
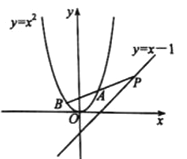
(1)当a+b=0时，求“优点”P的横坐标；
(2)若“优点”P的横坐标为3，求式子18a-9b的值；
(3)小安演算发现：直线y=x-1上的所有点都是“优点”，请判断小安发现是否正确？如果正确，说明理由；如果不正确，举出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
