
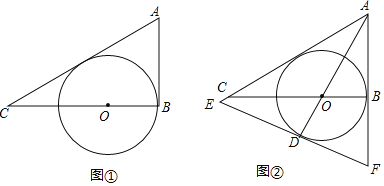
【题目】如图①,Rt△ABC中,∠ABC=90°,∠CAB的平分线交BC于点O,以O为圆心,OB长为半径作⊙O.
(1)求证:⊙O与AC相切.
(2)若AB=6,AC=10.
①求⊙O的半径;
②如图②,延长AO交⊙O于点D,过点D作⊙O的切线,分别交AC、AB的延长线于E、F,试求EF的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]()
【解析】
(1)根据角平分线的性质,可以证明本结论成立;
(2)①根据切线的性质可知AB=AM,根据勾股定理可以求得BC的长,进而可以求得圆的半径的长;
②根据题意可以求得AD的长,然后根据三角形相似可以求得DF的长,由等腰三角形的性质可以求得EF的长.
(1)证明:∵∠ABC=90°,∠CAB的平分线是AO,
∴点O到AB和到AC的距离相等,
∴点O到AC的距离等于圆O的半径,
∴⊙O与AC相切;
(2)①作OM⊥AC于点M,如图所示,

∵AB=6,AC=10,∠ABC=90°,
∴BC=8,AB=AM=6,
∴MC=4,OC=8-OB,
设圆O的半径是r,
∴r2+42=(8-r)2
解得,r=3,
即⊙O的半径是3;
②∵AB=6,BO=3,∠ABO=90°,
∴AO=3![]() ,
,
∴AD=3+3![]() ,
,
∵AD⊥EF,
∴∠ADF=90°,
∴∠ADF=∠ABO=90°,
∵∠DAF=∠BAO,
∴△DAF∽△BAO,
∴![]() ,
,
即![]() ,
,
解得,DF=![]() ,
,
∵AD平分∠EAF,AD⊥EF,
∴EF=2DF=3+3![]() .
.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
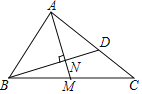
【题目】已知:如图,在△ABC中,∠BAC=90°,M是斜边BC的中点,BN⊥AM,垂足为点N,且BN的延长线交AC于点D.
(1)求证:△ABC∽△ADB;
(2)如果BC=20,BD=15,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
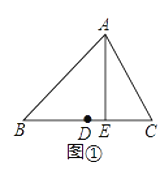
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
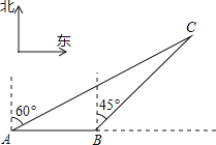
【题目】如图:007渔船在南海海面上沿正东方向匀速航行,在A点观测到渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若007渔船航向不变,航行半小时后到达B点,观测到渔船C在东北方向上.问:007渔船再按原航向航行多长时间,离渔船C的距离最近?
查看答案和解析>>
科目:初中数学 来源: 题型:
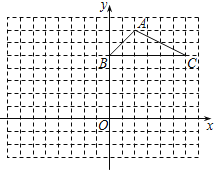
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶
点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 .
(2)将△ABC向左平移7个单位,请画出平移后的△A1B1C1.若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .
(3)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出△A2B2C2,并写出点A2的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |

成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农场有100棵果树,每一棵树平均结600个果子.现准备多种一些果树以提高产量,根据经验估计,每多种一棵果树,平均每棵树就会少结5个果子.假设果园增种x棵果树,果子总产量为y个.
(1)增种多少棵果树,可以使果园的总产量最多?最多为多少?
(2)增种多少棵果树,可以使果子的总产量在60400个以上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com