
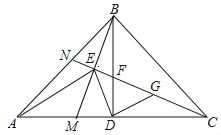
【题目】如图,等腰直角△ABC中,AB=BC,∠ABC=90°,BD⊥AC于D,点M在AD上,连接BM,过点C作CN⊥BM于点E,交AB于N,交BD于F,连接DE,AE.
(1)若∠BCN=30°,EN=2,求AN的长;
(2)若DE⊥AE于E,DG⊥DE交CN于G,求证:CE=![]() AE.
AE.
【答案】(1)4![]() -4(2)证明见解析
-4(2)证明见解析
【解析】
(1)根据∠ABC=90°,CN⊥BM可得∠EBN=∠BCN=30°,根据直角三角形的性质求出BN,再根据勾股定理求出BC的值,再根据AB=BC即可解决问题;
(2)根据等腰三角形的性质证出D为AC的中点证明,再根据AE⊥DE,DE⊥DG得出DG∥AE,进而证明DG=![]() AE,再证明△DEG是等腰直角三角形即可解决问题;
AE,再证明△DEG是等腰直角三角形即可解决问题;
(1)解:∵∠BCN=30°,∠CBN=90°,
∴∠CNB=60°,∵BE⊥CN,∴∠EBN=30°,
∵EN=2,∴BN=4,∴CN=8
∴BC=BA=4![]() ,
,
∴AN=AB﹣BN=4![]() ﹣4.
﹣4.
(2)∵BA=BC,BD⊥AC,
∴AD=DC=BD,
∵AE⊥DE,DE⊥DG,
∴∠AED=∠EDG=90°,
∴DG∥AE,
∴EG=GC,
∴DG=![]() AE,
AE,
∠EDG=∠BDC=90°,
∴∠BDE=∠CDG,
∵∠BEF=∠FDC=90°,∠BFE=∠CFD,
∴∠DBE=∠DCG,∵BD=CD,
∴△BDE≌△CDG,
∴DE=DG,
∴EG=![]() DG,
DG,
∴2EG=![]() (2DG),
(2DG),
即EC=![]() AE.
AE.


科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
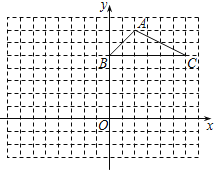
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶
点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 .
(2)将△ABC向左平移7个单位,请画出平移后的△A1B1C1.若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .
(3)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出△A2B2C2,并写出点A2的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
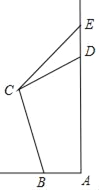
【题目】如图,我校本部教师楼AD上有“育才中学”四个字的展示牌DE,某数学兴趣小组的同学准备利用所学的三角函数知识估测该教师楼的高度,由于场地有限,不便测量,所以小明沿坡度i=![]() :1的阶梯从看台前的B处前行50米到达C处,测得展示牌底部D的仰角为45°,展示牌顶部E的仰角为53°(小明的身高忽略不计),已知展示牌高DE=15米,则该教师楼AD的高度约为( )米.(参考数据:Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75,
:1的阶梯从看台前的B处前行50米到达C处,测得展示牌底部D的仰角为45°,展示牌顶部E的仰角为53°(小明的身高忽略不计),已知展示牌高DE=15米,则该教师楼AD的高度约为( )米.(参考数据:Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75,![]() ≈1.7)
≈1.7)
A. 102.5B. 87.5C. 85D. 70
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |

成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
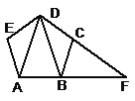
【题目】如图,正五边形ABCDE中,DC和AB的延长线交于F,则图中与△DBF相似的三角形有(不再添加其他的线段和字母,不包括△DBF本身) ( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com