
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图②,若∠ABC=120°,cos∠ADC=![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).

【答案】(1)详见解析;(2)18![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)证明△EAB∽△ECD,根据相似三角形的性质即可得结论;(2)过点C作CG⊥AD于点D,过点A作AH⊥BC于点H.在Rt△CDG中利用已知条件求得DG、OG的长,再根据△CDE的面积为6,可求得DE的长,在△ABH中求得BH、AH的长,利用(1)△EAB∽△ECD,可求得EH的长,由S四边形ABCD=S△AEH-S△ECD-S△ABH即可求得四边形ABCD的面积;(3)由(1)(2)提供的思路即可求解.
试题解析:
(1)证明:∵∠ADC=90°,
∴∠EDC=90°,
∴∠ABE=∠CDE.
又∵∠AEB=∠CED,
∴△EAB∽△ECD,
∴![]() =
=![]() ,
,
∴ED·EA=EC·EB.
(2)过点C作CG⊥AD于点D,过点A作AH⊥BC于点H.
∵CD=5,cos∠ADC=![]() ,
,
∴DG=3,CG=4.
∵S△CED=6,
∴ED=3,
∴EG=6.
∵AB=12,∠ABC=120°,则∠BAH=30°,
∴BH=6,AH=6![]() .
.
由(1)得△ECG∽△EAH,
∴![]() =
=![]() ,
,
∴EH=9![]() ,
,
∴S四边形ABCD=S△AEH-S△ECD-S△ABH=![]() ×6
×6![]() ×9
×9![]() -6-
-6-![]() ×6
×6![]() ×6=75-18
×6=75-18![]() .
.
(3)作CH⊥AD于H,则CH=4,DH=3.
∴tanE=![]() .作AG⊥DF于点G.
.作AG⊥DF于点G.
设AD=5a,则DG=3a,AG=4a,
∴FG=DF-DG=5+n-3a.
∵CH⊥AD,AG⊥DF,∠E=∠F,
∴△AFG∽△CEH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴a=![]() ,
,
∴AD=5a=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x+m)2+m与直线y=x相交于E,C两点(点E在点C的左边),抛物线与x轴交
于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
⑴ 若抛物线与y轴交点坐标为(0,2),求m的值;
⑵ 求证:⊙H与直线y=1相切;
⑶ 若DE=2EC,求⊙H的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
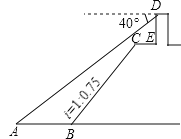
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2x3+32﹣32+5=(x+3)2﹣4,
∵(x+3)2≥0
∴当x=﹣3时,x2+6x+5有最小值﹣4.
请根据上述方法,解答下列问题:
(Ⅰ)x2+4x﹣1=x2+2x2+22﹣22﹣1=(x+a)2+b,则ab的值是_____;
(Ⅱ)求证:无论x取何值,代数式x2+2![]() x+7的值都是正数;
x+7的值都是正数;
(Ⅲ)若代数式2x2+kx+7的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
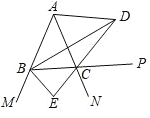
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上分别表示的数为-10,2,8,点D是BC中点,点E是AD中点.
(1)求EB的长;
(2)若动点P从点A出发,以1cm/s的速度向点C运动,达到点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
(3)点A,B,C开始在数轴上运动,若点A以1cm/s的速度向左运动,同时,点B和点C分别以4cm/s和9cm/s的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB-BC的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请求其常数值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com