
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
【答案】(1)8;(2)M(0,2)或(0,﹣2);(3)①∠APO=∠DOP+∠BAP;②∠DOP=∠BAP+∠APO;③∠BAP=∠DOP+∠APO.
【解析】
(1)先由非负数性质求出a=2,b=4,再根据平移规律,得出点C,D的坐标,然后根据四边形ABDC的面积=AB×OA即可求解;
(2)存在.设M坐标为(0,m),根据S△PAB=S四边形ABDC,列出方程求出m的值,即可确定M点坐标;
(3)分三种情况求解:①当点P在线段BD上移动时,②当点P在DB的延长线上时,③当点P在BD的延长线上时.
解:(1)∵(a﹣2)2+|b﹣4|=0,
∴a=2,b=4,
∴A(0,2),B(4,2).
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴C(﹣1,0),D(3,0).
∴S四边形ABDC=AB×OA=4×2=8;
(2)在y轴上存在一点M,使S△MCD=S四边形ABCD.设M坐标为(0,m).
∵S△MCD=![]() S四边形ABDC,
S四边形ABDC,
∴![]() ×4|m|=4,
×4|m|=4,
∴2|m|=4,
解得m=±2.
∴M(0,2)或(0,﹣2);
(3)①当点P在线段BD上移动时,∠APO=∠DOP+∠BAP
理由如下:
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
②当点P在DB的延长线上时,同①的方法得,∠DOP=∠BAP+∠APO;
③当点P在BD的延长线上时,同①的方法得,∠BAP=∠DOP+∠APO.


科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中给定以下五个点A(-2,0),B(1,0),C(4,0),D![]() ,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
(1)符合条件的抛物线共有多少条?不求解析式,请用约定的方法一一表示出来.
(2)在五个形状、颜色、质量完全相同的乒乓球上标上A,B,C,D,E代表以上五个点,玩摸球游戏,每次摸三个球.请问:摸一次,三球代表的点恰好能确定一条符合条件的抛物线的概率是多少?
(3)小强、小亮用上面的五球玩游戏,若符合要求的抛物线开口向上,小强可以得1分;若抛物线开口向下,小亮得5分,你认为这个游戏谁获胜的可能性大一些?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过(2,3)和(﹣1,﹣3),直线l2经过原点O,且与直线l1交于点P(﹣2,a).
(1)求a的值;
(2)(﹣2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点A,你能求出△APO的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形 如图,若运动方向相反,则称它们是镜面合同三角形 如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180° 如图,下列各组合同三角形中,是镜面合同三角形的是( )
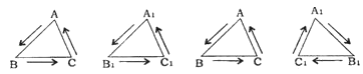
A.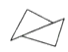 B.
B.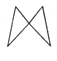 C.
C.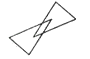 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于F.

(1)如图1,连CF,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°时,求证:AF+EF=FB;
(3)如图3,当∠ABC=45°时,若BD平分∠ABC,求证:BD=2EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com