
【题目】在平面直角坐标系中给定以下五个点A(-2,0),B(1,0),C(4,0),D![]() ,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
(1)符合条件的抛物线共有多少条?不求解析式,请用约定的方法一一表示出来.
(2)在五个形状、颜色、质量完全相同的乒乓球上标上A,B,C,D,E代表以上五个点,玩摸球游戏,每次摸三个球.请问:摸一次,三球代表的点恰好能确定一条符合条件的抛物线的概率是多少?
(3)小强、小亮用上面的五球玩游戏,若符合要求的抛物线开口向上,小强可以得1分;若抛物线开口向下,小亮得5分,你认为这个游戏谁获胜的可能性大一些?说说你的理由.
【答案】(1) ABE ACE BCD BCE BDE CDE;(2) ![]() ;(3)这个游戏两人获胜的可能性一样,理由解析.
;(3)这个游戏两人获胜的可能性一样,理由解析.
【解析】
(1)利用概率的知识可知道从A、B、C、D、E五个点中任意选取三点,共有10种组合,然后再根据条件选出6种情况;
(2)直接利用概率的求算方法求解即可;
(3)先判断这6条抛物线的开口方向再利用概率求算.
解:(1)从A,B,C,D,E五个点中任意选取三点,共有以下10种组合,分别如下:
ABC ABD ABE ACD ACE.
ADE BCD BCE BDE CDE.
∵A,D所在直线平行于y轴,A,B,C都在x轴上,
∴A,D不能在符合要求的同一条抛物线上,A,B,C也不能在符合要求的同一条抛物线上,
于是符合条件的抛物线有如下六条:
ABE ACE BCD BCE BDE CDE
(2)摸一次,三球代表的点恰好能确定一条符合条件的抛物线的概率为![]() .
.
(3)这个游戏两人获胜的可能性一样.
理由是:在可以确定的六条抛物线中,通过观察五点位置可知:抛物线BCE开口向下,其余五条开口向上,每摸一次,
小强获得分数的平均值为![]() ×1=
×1=![]() ;
;
小亮获得分数的平均值为![]() ×5=
×5=![]() ,
,
∴这个游戏两人获胜的可能性一样.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
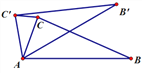
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
A. 70° B. 35° C. 40° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2﹣3x的图象经过O(0,0),A(4,4),B(3,0)三点,以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,得到△OA′B′,二次函数y=ax2+bx+c(a≠0)的图象经过O,A′,B′三点.
(1)画出△OA′B′,试求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)点P(m,n)在二次函数y=x2﹣3x的图象上,m≠0,直线OP与二次函数y=ax2+bx+c(a≠0)的图象交于点Q(异于点O).
①连接AP,若2AP>OQ,求m的取值范围;
②当点Q在第一象限内,过点Q作QQ′平行于x轴,与二次函数y=ax2+bx+c(a≠0)的图象交于另一点Q′,与二次函数y=x2﹣3x的图象交于点M,N(M在N的左侧),直线OQ′与二次函数y=x2﹣3x的图象交于点P′.△Q′P′M∽△QB′N,则线段 NQ的长度等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是________.(只写出符合要求的一个即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com