
【题目】如图,二次函数y=x2﹣3x的图象经过O(0,0),A(4,4),B(3,0)三点,以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,得到△OA′B′,二次函数y=ax2+bx+c(a≠0)的图象经过O,A′,B′三点.
(1)画出△OA′B′,试求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)点P(m,n)在二次函数y=x2﹣3x的图象上,m≠0,直线OP与二次函数y=ax2+bx+c(a≠0)的图象交于点Q(异于点O).
①连接AP,若2AP>OQ,求m的取值范围;
②当点Q在第一象限内,过点Q作QQ′平行于x轴,与二次函数y=ax2+bx+c(a≠0)的图象交于另一点Q′,与二次函数y=x2﹣3x的图象交于点M,N(M在N的左侧),直线OQ′与二次函数y=x2﹣3x的图象交于点P′.△Q′P′M∽△QB′N,则线段 NQ的长度等于 .

【答案】(1)二次函数的解析式为y=![]() x2﹣3x;(2)①1﹣
x2﹣3x;(2)①1﹣![]() <m<1+
<m<1+![]() ,且m≠0;②6
,且m≠0;②6
【解析】
(1)根据位似的性质得出A′(8,8),B′(6,0),将O(0,0),A′(8,8),B′(6,0)代入y=ax2+bx+c,利用待定系数法进行求解即可得;
(2)①如图1,由P(m,n)在二次函数y=x2﹣3x的图象上,可得P(m,m2﹣3m),根据待定系数法易求得OP的解析是为y=(m﹣3)x,继而可求得Q(2m,2m2﹣6m),过点P作PC⊥x轴于点C,过点Q作QD⊥x轴于点D,证明△OCP∽△ODQ,可得OQ=2OP,然后根据2AP>OQ,可得AP>OP,从而可得关于m的不等式,解不等式即可得;
②如图2,P(m,m2﹣3m),Q(2m,2m2﹣6m),根据点Q在第一象限,可得m>3,QQ′的表达式是y=2m2﹣6m,解方程组 ,可得点Q′(6﹣2m,2m2﹣6m),继而可得OQ′的解析式为y=﹣mx,从而求得点P′(3﹣m,m2﹣3m),由QQ′与y=x2﹣3x交于点M、N,求出点M、N的坐标,再根据△Q′P′M∽△QB′N,根据相似三角形的性质可得关于的方程,解方程求出m的值即可得答案.
,可得点Q′(6﹣2m,2m2﹣6m),继而可得OQ′的解析式为y=﹣mx,从而求得点P′(3﹣m,m2﹣3m),由QQ′与y=x2﹣3x交于点M、N,求出点M、N的坐标,再根据△Q′P′M∽△QB′N,根据相似三角形的性质可得关于的方程,解方程求出m的值即可得答案.
(1)如图1,由以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,
得![]() ,
,
∵A(4,4),B(3,0),
∴A′(8,8),B′(6,0),
将O(0,0),A′(8,8),B′(6,0)代入y=ax2+bx+c,
得 ,解得
,解得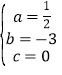 ,
,
∴二次函数的解析式为y=![]() x2﹣3x;
x2﹣3x;
(2)①如图1,∵P(m,n)在二次函数y=x2﹣3x的图象上,
∴n=m2﹣3m,
∴P(m,m2﹣3m),
设直线OP的解析式为y=kx,将点P(m,m2﹣3m)代入函数解析式,
得mk=m2﹣3m,
∴k=m﹣3,
∴OP的解析是为y=(m﹣3)x,
∵OP与y═![]() x2﹣3x交于Q点,
x2﹣3x交于Q点,
∴ ,解得
,解得![]() (不符合题意舍去),
(不符合题意舍去), ,
,
∴Q(2m,2m2﹣6m),
过点P作PC⊥x轴于点C,过点Q作QD⊥x轴于点D,
则OC=|m|,PC=|m2﹣3m|,OD=|2m|,QD=|2m2﹣6m|,
∵![]() ,
,
∴△OCP∽△ODQ,
∴OQ=2OP,
∵2AP>OQ,
∴2AP>2OP,即AP>OP,
∴![]() ,
,
化简,得m2﹣2m﹣4<0,解得1﹣![]() <m<1+
<m<1+![]() ,且m≠0;
,且m≠0;
②如图2,P(m,m2﹣3m),Q(2m,2m2﹣6m)
∵点Q在第一象限,
∴![]() ,解得m>3,
,解得m>3,
由Q(2m,2m2﹣6m),得QQ′的表达式是y=2m2﹣6m,
∵QQ′′交y=![]() x2﹣3x交于点Q′,
x2﹣3x交于点Q′,
 ,解得
,解得 (不符合题意,舍),
(不符合题意,舍), ,
,
∴Q′(6﹣2m,2m2﹣6m),
设OQ′的解析是为y=kx,(6﹣2m)k=2m2﹣6m,
解得k=﹣m,OQ′的解析式为y=﹣mx,
∵OQ′与y=x2﹣3x交于点P′,
∴﹣mx=x2﹣3x,
解得x1=0(舍),x2=3﹣m,
∴P′(3﹣m,m2﹣3m),
∵QQ′与y=x2﹣3x交于点M、N,
∴x2﹣3x=2m2﹣6m,
解得x1=![]() ,x2=
,x2=![]() ,
,
∵M在N左侧,
∴M(![]() ,2m2﹣6m),N(
,2m2﹣6m),N(![]() ,2m2﹣6m),
,2m2﹣6m),
∵△Q′P′M∽△QB′N,
∴![]() ,
,
∵![]() ,
,
即 ,
,
化简得:m2﹣12m+27=0,
解得:m1=3(舍),m2=9,
∴N(12,108),Q(18,108),
∴QN=6,
故答案为:6.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】有一个抛两枚硬币的游戏,规则是:若出现两个正面,则甲赢;若出现一正一反,则乙赢;若出现两个反面,则甲、乙都不赢。
(1)这个游戏是否公平?请说明理由;
(2)如果你认为这个游戏不公平,那么请你改变游戏规则,设计一个公平的游戏;如果你认为这个游戏公平,那么请你改变游戏规则,设计一个不公平的游戏。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中给定以下五个点A(-2,0),B(1,0),C(4,0),D![]() ,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
(1)符合条件的抛物线共有多少条?不求解析式,请用约定的方法一一表示出来.
(2)在五个形状、颜色、质量完全相同的乒乓球上标上A,B,C,D,E代表以上五个点,玩摸球游戏,每次摸三个球.请问:摸一次,三球代表的点恰好能确定一条符合条件的抛物线的概率是多少?
(3)小强、小亮用上面的五球玩游戏,若符合要求的抛物线开口向上,小强可以得1分;若抛物线开口向下,小亮得5分,你认为这个游戏谁获胜的可能性大一些?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过(2,3)和(﹣1,﹣3),直线l2经过原点O,且与直线l1交于点P(﹣2,a).
(1)求a的值;
(2)(﹣2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点A,你能求出△APO的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于48棵,且用于购买这两种树的资金不能超过7500元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形 如图,若运动方向相反,则称它们是镜面合同三角形 如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180° 如图,下列各组合同三角形中,是镜面合同三角形的是( )
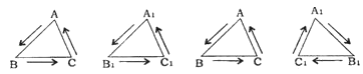
A. B.
B. C.
C.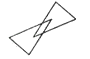 D.
D.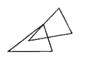
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有 .(把正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.

求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,

①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com