
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
【答案】(1)证明见解析(2)y=x2+2x﹣3(3)![]()
【解析】试题分析:(1)证明抛物线的对称轴<0即可证明抛物线的对称轴在y轴的左侧;
(2)根据题中已知条件求出m的值,进而求得抛物线的解析式;
(3)先设出C点坐标,根据的x1与x2关系求出m值,进而可求得△ABC的面积.
解:(1)证明:∵m>0,
∴x=﹣![]() =﹣
=﹣![]() <0,
<0,
∴抛物线的对称轴在y轴的左侧;
(2)设抛物线与x轴交点为A(x1,0),B(x2,0),
则x1+x2=﹣m<0,x1x2=﹣![]() m2<0,
m2<0,
∴x1与x2异号,
又∵![]() >0,
>0,
∴OA>OB,
由(1)知:抛物线的对称轴在y轴的左侧,
∴x1<0,x2>0,
∴OA=|x1|=﹣x1 ,
OB=x2,
代入![]() 得:
得: ![]() ,
,
![]() ,
,
从而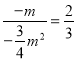 ,
,
解得m=2,
经检验m=2是原方程的根,
∴抛物线的解析式为y=x2+2x﹣3;
(3)解:当x=0时,y=﹣![]() m2
m2
∴点C(0,﹣ ![]() m2),
m2),
∵△ABC是直角三角形,
∴AB2=AC2+BC2,
∴(x1﹣x2)2=x12+(﹣![]() m2)2+x22+(﹣
m2)2+x22+(﹣![]() m2)2
m2)2
∴﹣2x1x2=![]() m4
m4
∴﹣2(﹣![]() mspan>2)=
mspan>2)=![]() m4,
m4,
解得m=![]() ,
,
∴S△ABC=![]() ×ABOC=
×ABOC=![]() |x1﹣x2||﹣
|x1﹣x2||﹣![]() m2|=
m2|=![]() ×2m×
×2m×![]() m2=
m2=![]() .
.


科目:初中数学 来源: 题型:
【题目】2007年5月19日起,中国人民银行上调存款利率.
人民币存款利率调整表:
项 目 | 调整前年利率% | 调整后年利率% |
活期存款 | 0.72 | 0.72 |
二年期定期存款 | 2.79 | 3.06 |
储户的实得利息收益是扣除利息税后的所得利息,利息税率为20%.
(1)小明于2007年5月19日把3500元的压岁钱按一年期定期存入银行,到期时他实得利息收益是多少元?
(2)小明在这次利率调整前有一笔一年期定期存款,到期时按调整前的年利率2.79%计息,本金与实得利息收益的和为2555.8元,问他这笔存款的本金是多少元?
(3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
约定:①存款天数按整数天计算,一年按360天计算利息.
②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存,利息按调整前的一年期定期利率计算;如果转存,转存前已存天数的利息按活期利率计算,转存后,余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求出符合条件的二次函数解析式:
(1)二次函数图象经过点(﹣1,0),(1,2),(0,3);
(2)二次函数图象的顶点坐标为(﹣3,6),且经过点(﹣2,10);
(3)二次函数图象与x轴的交点坐标为(﹣1,0),(3,0),与y轴交点的纵坐标为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
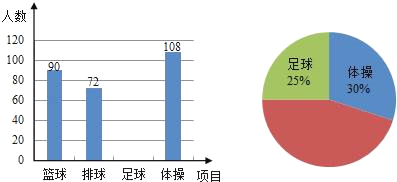
【题目】某中学进行体育教学改革,同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一,体育老师根据七年级学生的报名情况进行了统计,并绘制了下面尚未完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)该校七年级共有多少名学生?
(2)将两个统计图补充完整;
(3)从统计图中你还能得到哪些信息?(写出两条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知开始输入的x的值为正整数.若最后输出的结果为144,则满足条件的x的值为________;若经过一次运算就能输出结果,则x的最小值为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)= ;
(3)盒子中有黑球 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
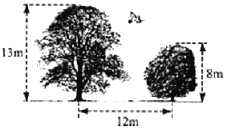
【题目】如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com