
【题目】某中学进行体育教学改革,同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一,体育老师根据七年级学生的报名情况进行了统计,并绘制了下面尚未完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)该校七年级共有多少名学生?
(2)将两个统计图补充完整;
(3)从统计图中你还能得到哪些信息?(写出两条即可)
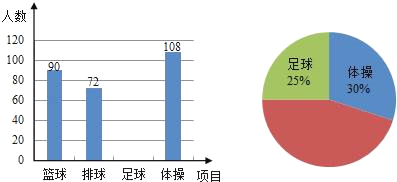
【答案】(1)该校九年级共有360名学生;(2)补全的两个统计图见解析;(3)
1、七年级学生选学体操的人数最多;
2、七年级学生选学排球的人数最少;
3、25%(或![]() );
);
4、25%(或![]() ).
).
【解析】试题分析:(1)由统计图得,选体操的人数与其所占的比例;根据百分比的意义可得关系式并计算可得答案;
(2)由(1)可得总人数,进而可得报足球的人数,根据得到的信息可以补全两个统计图;
(3)开放性题目,根据题意,结合条形统计图;可得信息,答案不唯一;合理即可.
试题解析:(1)由统计图得,108÷30%=360,故该校九年级共有360名学生.
(2)补全的两个统计图如下:
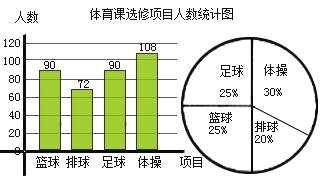
(3)1、七年级学生选学体操的人数最多;
2、七年级学生选学排球的人数最少;
3、选学篮球的人数是九年级学生总人数的25%;
4、选学足球的人数是九年级学生总人数的25%.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
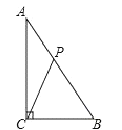
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A. 5 B. 5或8 C. ![]() D. 4或
D. 4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
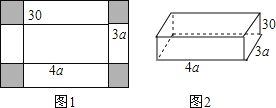
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.

(1)填空:甲厂的制版费是________千元,当x≤2(千个)时乙厂证书印刷单价是________元/个;
(2)求出甲厂的印刷费y甲与证书数量x的函数关系式,并求出其证书印刷单价;
(3)当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂计划生产A,B两款校服共500件,这两款校服的成本、售价如表所示:
类别 | 成本(元/件) | 售价(元/件) |
A款 | 30 | 45 |
B款 | 50 | 70 |
(1)求校服厂家销售完这批校服时所获得的利润y(元)与A款校服的生产数量x(件)之间的函数关系.
(2)若厂家计划B款校服的生产数量不超过A款校服的生产数量的4倍,应怎样安排生产才能使校服厂家在销售完这批校服时获得利润最多?此时获得利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com