
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
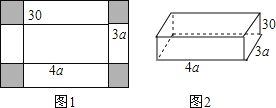
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
【答案】(1)12a2+420a+3600;
(2)600a+21000(元);
(3)a=105;
(4)存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.
【解析】
试题分析:(1)根据图形表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)用铁盒的底面积除以全面积即可得出底面积是全面积的几分之几,再根据铁盒的底面积是全面积的![]() ,求出a的值即可;
,求出a的值即可;
(4)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.
解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷![]() =(12a2+420a)×
=(12a2+420a)×![]() =600a+21000(元);
=600a+21000(元);
(3)铁盒的底面积是全面积的![]() =
=![]() ;
;
根据题意得:![]() =
=![]() ,
,
解得a=105;
(4)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是12a2,
假设存在正整数n,使12a2+420a=n(12a2)
则(n﹣1)a=35,
则a=35,n=2或a=7,n=6或a=5,n=8或a=1,n=36
所以存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
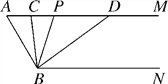
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x | … |
| 0 | 1 | 2 | … |
y | … |
|
|
|
| … |
A. y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() B. y=
B. y=![]() x2+
x2+![]() x﹣
x﹣![]()
C. y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() D. y=﹣
D. y=﹣![]() x2+
x2+![]() x+
x+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
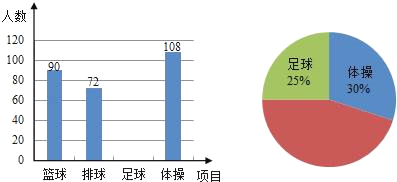
【题目】某中学进行体育教学改革,同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一,体育老师根据七年级学生的报名情况进行了统计,并绘制了下面尚未完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)该校七年级共有多少名学生?
(2)将两个统计图补充完整;
(3)从统计图中你还能得到哪些信息?(写出两条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解一元二次方程
(1)4x2﹣8x+1=0(配方法) (2)7x(5x+2)=6(5x+2)(因式分解法)
(3)3x2+5(2x+1)=0(公式法) (4)x2﹣2x﹣8=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com