
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
【答案】(1)y甲、y乙与x的函数关系式分别为:y甲=700x+2000,y乙=800x+1600;(2)当学生人数超过4人时,选择甲旅行社更省钱,当学生人数少于4人时,选择乙旅行社更省钱,学生人数等于4人时,选择甲、乙旅行社相等.
【解析】试题分析:(1)根据甲旅行社的收费=两名家长的全额费用+学生的七折费用,可得到y1与x的函数关系式;再根据乙旅行社的收费=两名家长的八折费用+学生的八折费用,可得到y2与x的函数关系式;
(2)根据题意知:y甲<y乙时,可以确定学生人数,选择甲旅行社更省钱.
试题解析:(1)、![]() =700x+2000
=700x+2000
![]() =800x+1600
=800x+1600
(2)、当![]() <
<![]() 时,
时,
即:700x+2000<800x+1600
∴x>4
答:当学生人数超过4人时,选择甲旅行社更省钱。
考点: 一次函数的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
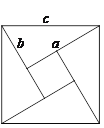
【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为![]() ,较短的直角边为
,较短的直角边为![]() ,斜边长为
,斜边长为![]() ,试利用图①验证勾股定理;
,试利用图①验证勾股定理;
(2)如图②,将这四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为![]() ,
, ![]() ,求该飞镖状图案的面积;
,求该飞镖状图案的面积;
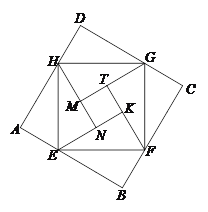
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面积分别为
的面积分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则
,则![]() =________.
=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
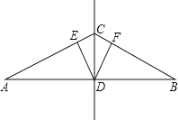
【题目】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
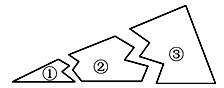
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
12
【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
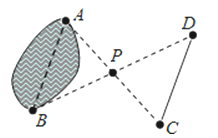
查看答案和解析>>
科目:初中数学 来源: 题型:
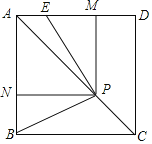
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
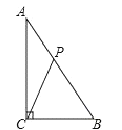
A. 5 B. 5或8 C. ![]() D. 4或
D. 4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
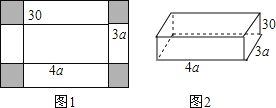
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com