
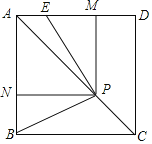
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)先证四边形PMAN是矩形,再证PM=PN;
(2)用ASA证明△EPM≌△BPN.
试题解析:
(1)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AC平分∠BAD,
∵PM⊥AD,PN⊥AB,∴PM=PN,∠PMA=∠PNA=90°,
∴四边形PMAN是矩形,
∵PM=PN,∴四边形PMAN是正方形;
(2)证明:∵四边形PMAN是正方形,∴PM=PN,∠MPN=90°,
∵∠EPB=90°,∴∠MPE+∠EPN=∠NPB+∠EPN=90°,∴∠MPE=∠NPB,
在△EPM和△BPN中,
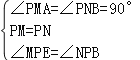 ,
,
∴△EPM≌△BPN(ASA),
∴EM=BN.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=∠COD=90°,射线OE,FO分别平分∠AOC和∠BOD.
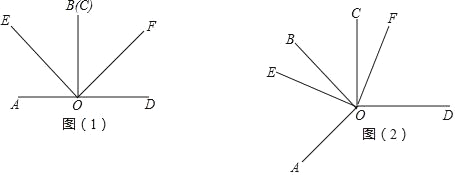
(1)当OB和OC重合时,如图(1),求∠EOF的度数;
(2)当∠AOB绕点O逆时针旋转至图(2)的位置(0°<∠BOC<90°)时,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
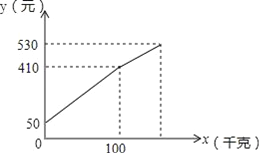
(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
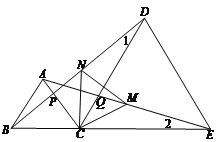
【题目】线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
(3)取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2007年5月19日起,中国人民银行上调存款利率.
人民币存款利率调整表:
项 目 | 调整前年利率% | 调整后年利率% |
活期存款 | 0.72 | 0.72 |
二年期定期存款 | 2.79 | 3.06 |
储户的实得利息收益是扣除利息税后的所得利息,利息税率为20%.
(1)小明于2007年5月19日把3500元的压岁钱按一年期定期存入银行,到期时他实得利息收益是多少元?
(2)小明在这次利率调整前有一笔一年期定期存款,到期时按调整前的年利率2.79%计息,本金与实得利息收益的和为2555.8元,问他这笔存款的本金是多少元?
(3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
约定:①存款天数按整数天计算,一年按360天计算利息.
②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存,利息按调整前的一年期定期利率计算;如果转存,转存前已存天数的利息按活期利率计算,转存后,余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
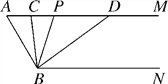
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com