
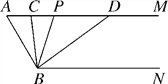
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
【答案】(1)60°;(2)不变,∠APB∶∠ADB=2∶1.,理由见解析;(3)∠ABC=30°
【解析】(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
解:(1)∵AM∥BN,∠A=60°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°.
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
(2)不变,∠APB∶∠ADB=2∶1.理由如下,
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB∶∠ADB=2∶1.
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN.
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
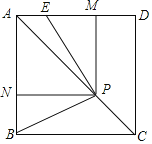
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
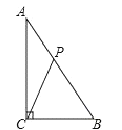
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A. 5 B. 5或8 C. ![]() D. 4或
D. 4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如下表:
小明家 | 爷爷家 | |
屋顶收集雨水的面积/m2 | 160 | 120 |
蓄水池的容积/ m3 | 50 | 13 |
蓄水池已有水的量/ m3 | 34 | 11.5 |
气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的
水注入小明家的蓄水池?
查看答案和解析>>
科目:初中数学 来源: 题型:
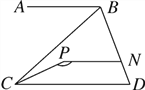
【题目】如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
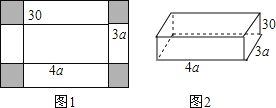
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com