【题目】如图，已知AB∥PN∥CD.
(1)试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；
(2)若∠ABC＝42°，∠CPN＝155°，求∠BCP的度数．
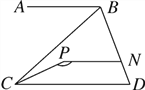
【答案】(1)见解析；（2）17°
【解析】试题分析：（1）由平行线的性质得出∠ABC=∠BMN=∠BCD，∠CPN+∠PCD=180°，即可得出结论；
（2）由（1）的结论代入计算即可．
试题解析：（1）∠ABC-∠BCP+∠CPN=180°；理由如下：
延长NP交BC于M，如图所示：
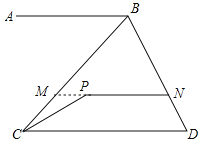
∵AB∥PN∥CD，
∴∠ABC=∠BMN=∠BCD，∠CPN+∠PCD=180°，
∵∠PCD=∠BCD-∠BCP=∠ABC-∠BCP，
∴∠ABC-∠BCP+∠CPN=180°．
（2）由（1）得：∠ABC-∠BCP+∠CPN=180°，
则∠BCP=∠ABC+∠CPN-180°=155°+42°-180°=17°．
百年学典课时学练测系列答案科目：初中数学 来源： 题型：
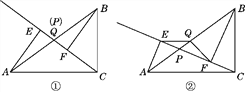
【题目】已知点P是Rt△ABC斜边AB上一动点(不与点A，B重合)，分别过点A，B向直线CP作垂线，垂足分别为点E，F，点Q为斜边AB的中点．
(1)如图①，当点P与点Q重合时，AE与BF的位置关系是________，QE与QF的数量关系是________；
(2)如图②，当点P在线段AB上且不与点Q重合时，试判断QE与QF的数量关系，并说明理由．
(温馨提示：直角三角形斜边上的中线等于斜边的一半)
查看答案和解析>>
科目：初中数学 来源： 题型：
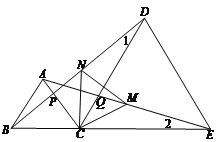
【题目】线段BE上有一点C，以BC，CE为边分别在BE的同侧作等边三角形ABC，DCE，连接AE，BD，分别交CD，CA于Q，P.
（1）找出图中的所有全等三角形.
（2）找出一组相等的线段，并说明理由.
（3）取AE的中点M、BD的中点N，连接MN，试判断三角形CMN的形状，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：
若a，b都是非负实数，则a＋b≥2
.当且仅当a＝b时，“＝”成立．
证明： ∵(
－
)2≥0，∴a－2
＋b≥0.
∴a＋b≥2
.当且仅当a＝b时，“＝”成立．
举例应用：
已知x>0，求函数y＝2x＋
的最小值．
解：y＝2x＋
≥2
＝4.当且仅当2x＝
，即x＝1时，“＝”成立．
当x＝1时，函数取得最小值，y最小＝4.
问题解决：
汽车的经济时速是指汽车最省油的行驶速度．某种汽车在每小时70～110公里之间行驶(含70公里和110公里)，每公里耗油(
＋
)升．若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
(1)求y关于x的函数关系式(写出自变量x的取值范围)；
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AM∥BN，∠A＝60°，点P是射线AM上一动点(与A不重合)，BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C、D.
(1)求∠CBD的度数；
(2)当点P运动时，∠APB∶∠ADB的度数比值是否发生变化？若不变，请求出这个比值；若变化，请找出变化规律；
(3)当点P运动到使∠ACB＝∠ABD时，求∠ABC的度数．
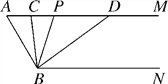
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D是AB上一点，DF交AC于点E，AE＝EC，DE＝EF，则下列说法中：①∠ADE＝∠EFC；②∠ADE＋∠ECF＋∠FEC＝180°；③∠B＋∠BCF＝180°；④S△ABC＝S四边形DBCF.正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值，可判断二次函数的解析式为（ ）
x | … |
| 0 | 1 | 2 | … |
y | … |
|
|
|
| … |
A. y=
x2﹣
x﹣
B. y=
x2+
x﹣
C. y=﹣
x2﹣
x+
D. y=﹣
x2+
x+
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．
试验种子n（粒） | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
（1）计算表中a，b的值；
（2）估计该麦种的发芽概率；
（3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
