
【题目】已知点P是Rt△ABC斜边AB上一动点(不与点A,B重合),分别过点A,B向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是________,QE与QF的数量关系是________;
(2)如图②,当点P在线段AB上且不与点Q重合时,试判断QE与QF的数量关系,并说明理由.
(温馨提示:直角三角形斜边上的中线等于斜边的一半)
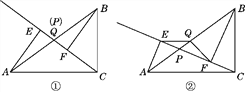
【答案】(1)AE∥BF,QE=QF;(2) QE=QF,理由见解析.
【解析】试题分析:(1)、根据AAS推出△AEQ和△BFQ全等即可得出答案;(2)、延长EQ交BF于D,求出△AEQ和△BDQ全等,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.
试题解析:(1)、如图1,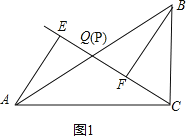
当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE=QF,
理由:∵Q为AB的中点, ∴AQ=BQ, ∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,∴△AEQ≌△BFQ, ∴QE=QF;
(2)、QE=QF证明:如图2,延长EQ交BF于D,
∵由(1)知:AE∥BF, ∴∠AEQ=∠BDQ, ∴△AEQ≌△BDQ, ∴EQ=DQ,
∵∠BFE=90°, ∴QE=QF.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.
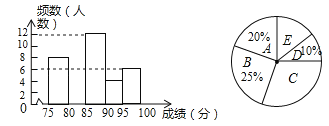
请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过15吨(含15吨)时,每吨按政府补贴优惠价收费;每月超过15吨时,超过部分每吨按市场调节价收费.小明家1月份用水23吨,交水费35元,2月份用水19吨,交水费25元.
(1)求每吨水的政府补贴优惠价与市场调节价分别是多少;
(2)小明家3月份用水24吨,他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
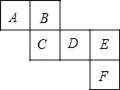
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
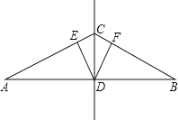
【题目】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
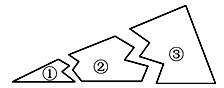
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
12
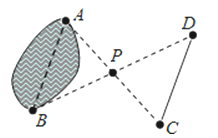
【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
查看答案和解析>>
科目:初中数学 来源: 题型:
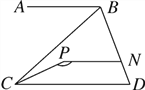
【题目】如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com