【题目】AB是⊙O的直径，AC、AD是⊙O的两弦，已知AB=16，AC=8，AD=
，求∠DAC的度数．
【答案】（1）30°（2）90°
【解析】试题分析：过O作OE⊥AC于E，OF⊥AD于F，根据垂径定理求出AE、AF，解直角三角形求出∠CAB和∠DAB，即可得出答案．
试题解析：解：过O作OE⊥AC于E，OF⊥AD于F，∵AC=8，AD=8
，∴由垂径定理得：AE=CE=4，AF=DF=4，∵AB=16，∴OA=8，在Rt△AEO中，∠AEO=90°，cos∠CAB=
=
=
，所以∠CAB=60°，在Rt△AFO中，∠AFO=90°，cos∠DAB=
=
=
，所以∠DAB=30°，图1中∠DAC=∠CAB+∠DAB=60°+30°=90°；
图2中∠DAC=∠CAB﹣∠DAB=60°﹣30°=30°；
即∠DAC的度数是90°或30°．
科目：初中数学 来源： 题型：
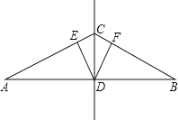
【题目】如图，点D是线段AB的中点，点C是线段AB的垂直平分线上的任意一点，DE⊥AC于点E，DF⊥BC于点F．
（1）求证：CE=CF；
（2）点C运动到什么位置时，四边形CEDF成为正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
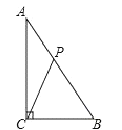
【题目】如图，在△ABC中，已知∠ACB=90°，AB=10cm，AC=8cm，动点P从点A出发，以2cm/s的速度沿线段AB向点B运动．在运动过程中，当△APC为等腰三角形时，点P出发的时刻t可能的值为（ ）
A. 5 B. 5或8 C. 
D. 4或
查看答案和解析>>
科目：初中数学 来源： 题型：
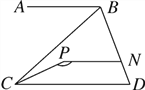
【题目】如图，已知AB∥PN∥CD.
(1)试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；
(2)若∠ABC＝42°，∠CPN＝155°，求∠BCP的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】云南地区地震发生后，市政府筹集了必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节省运费，市政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为14辆，你能求出这三种车型分别有多少辆吗？此时的运费又是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一张如图1的长方形铁皮，四个角都剪去边长为30厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2，铁盒底面长方形的长是4a（cm），宽是3a（cm），这个无盖铁盒各个面的面积之和称为铁盒的全面积．
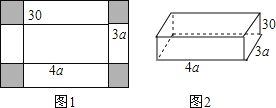
（1）请用a的代数式表示图1中原长方形铁皮的面积；
（2）若要在铁盒的各个外表面漆上某种油漆，每元钱可漆的面积为
（cm2），则油漆这个铁盒需要多少钱（用a的代数式表示）？
（3）铁盒的底面积是全面积的几分之几（用a的代数式表示）？若铁盒的底面积是全面积的
，求a的值；
（4）是否存在一个正整数a，使得铁盒的全面积是底面积的正整数倍？若存在，请求出这个a，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．
（1）填空：甲厂的制版费是________千元，当x≤2（千个）时乙厂证书印刷单价是________元/个；
（2）求出甲厂的印刷费y甲与证书数量x的函数关系式，并求出其证书印刷单价；
（3）当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于
的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com