练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．

    试验种子n（粒）

    1

    5

    50

    100

    200

    500

    1000

    2000

    3000

    发芽频数m

    1

    4

    45

    92

    188

    476

    951

    1900

    2850

    发芽频率

    0

    0.80

    0.90

    0.92

    0.94

    0.952

    0.951

    a

    b

    （1）计算表中a，b的值；

    （2）估计该麦种的发芽概率；

    （3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？

    【答案】（1）0.95，0.95（2）0.95（3）82.65kg

    【解析】因为发芽频率=,所以；

    根据图表可知发芽频率趋于0.95平稳，故估计麦种发芽的概率为0.95；

    因为该麦种发芽后，只有87%的麦芽可以成活，所以可成活麦种质量为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

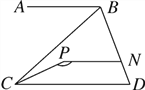
    【题目】如图，已知AB∥PN∥CD.

    (1)试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；

    (2)若∠ABC＝42°，∠CPN＝155°，求∠BCP的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．

    （1）填空：甲厂的制版费是________千元，当x≤2（千个）时乙厂证书印刷单价是________元/个；

    （2）求出甲厂的印刷费y甲与证书数量x的函数关系式，并求出其证书印刷单价；

    （3）当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某服装厂计划生产A，B两款校服共500件，这两款校服的成本、售价如表所示：

    价格

    类别

    成本（元/件）

    售价（元/件）

    A款

    30

    45

    B款

    50

    70

    （1）求校服厂家销售完这批校服时所获得的利润y（元）与A款校服的生产数量x（件）之间的函数关系．

    （2）若厂家计划B款校服的生产数量不超过A款校服的生产数量的4倍，应怎样安排生产才能使校服厂家在销售完这批校服时获得利润最多？此时获得利润为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连接OM、ON.

    （1）求图①中∠MON的度数；

    （2）图②中∠MON的度数是_________，图③中∠MON的度数是___________；

    （3）试探究∠MON的度数与正n边形边数n的关系（直接写出答案）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1+∠2=180°，∠B=∠3，你能判断∠C与∠AED的大小关系吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）

    A. 2 B. 4 C. 6 D. 8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线y=kx+b与反比例函数y=（x＞0）的图象分别交于点 A（m，3）和点B（6，n），与坐标轴分别交于点C和点D．

    （1）求直线AB的解析式；

    （2）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现定义一种新运算：“※”，使得a※b=4ab

    （1）求4※7的值；

    （2）求x※x+2※x﹣2※4=0中x的值；

    （3）不论x是什么数，总有a※x=x，求a的值．

    查看答案和解析>>

    同步练习册答案