
【题目】已知,∠AOB=∠COD=90°,射线OE,FO分别平分∠AOC和∠BOD.
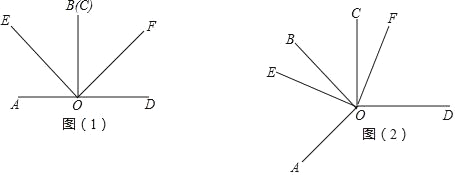
(1)当OB和OC重合时,如图(1),求∠EOF的度数;
(2)当∠AOB绕点O逆时针旋转至图(2)的位置(0°<∠BOC<90°)时,求∠EOF的度数.
【答案】(1)90°;(2)90°.
【解析】整体分析:
(1)根据角平分线的定义和平角的定义求解;(2)根据角平分线的定义和角的和差关系求解;
解:(1)当OB和OC重合时,∠AOD=∠AOC+∠BOD=180°,
又∵射线OE,FO分别平分∠AOC和∠BOD,
∴∠COE=![]() ∠AOC,∠BOF=
∠AOC,∠BOF=![]() ∠BOD,
∠BOD,
∴∠EOF=∠COF+∠BOF=![]() (∠AOC+∠BOD)=
(∠AOC+∠BOD)=![]() ×180°=90°;
×180°=90°;
(2)∵∠AOB=∠COD=90°,∠COE=![]() ∠AOC,∠BOF=
∠AOC,∠BOF=![]() ∠BOD,
∠BOD,
∴∠EOF=∠COE+∠BOF﹣∠BOC
=![]() ∠AOC+
∠AOC+![]() ∠BOD﹣∠BOC
∠BOD﹣∠BOC
=![]() (∠AOC+∠BOD)﹣∠BOC
(∠AOC+∠BOD)﹣∠BOC
=![]() (∠AOB+∠BOC+∠COD+∠BOC)﹣∠BOC
(∠AOB+∠BOC+∠COD+∠BOC)﹣∠BOC
=![]() (180°+2∠BOC)﹣∠BOC
(180°+2∠BOC)﹣∠BOC
=90°+∠BOC﹣∠BOC
=90°.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
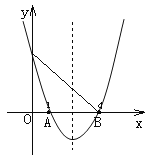
(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;![]() =_________,
=_________,![]() =________.
=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:

①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
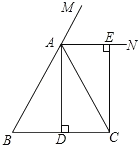
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
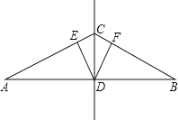
【题目】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
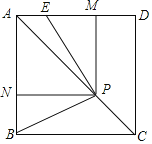
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com