
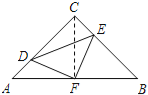
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:

①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
【答案】B
【解析】试题分析:解此题的关键在于判断△DEF是否为等腰直角三角形,作常规辅助线连接CF,由SAS定理可证△CFE和△ADF全等,从而可证∠DFE=90°,DF=EF.所以△DEF是等腰直角三角形.可证①正确,②错误,再由割补法可知④是正确的;
判断③,⑤比较麻烦,因为△DEF是等腰直角三角形DE=![]() DF,当DF与BC垂直,即DF最小时,DE取最小值4
DF,当DF与BC垂直,即DF最小时,DE取最小值4![]() ,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
解:连接CF;
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF(SAS);
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形(故①正确).
当D、E分别为AC、BC中点时,四边形CDFE是正方形(故②错误).
∵△ADF≌△CEF,
∴S△CEF=S△ADF∴S四边形CEFD=S△AFC,(故④正确).
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时DF=![]() BC=4.
BC=4.
∴DE=![]() DF=4
DF=4![]() (故③错误).
(故③错误).
当△CDE面积最大时,由④知,此时△DEF的面积最小.
此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8(故⑤正确).
故选:B.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
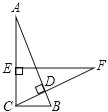
【题目】如图,Rt△ABC中,∠ACB=90°, BC=3cm, CD⊥AB于D, 在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=∠COD=90°,射线OE,FO分别平分∠AOC和∠BOD.
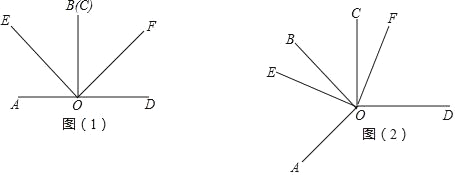
(1)当OB和OC重合时,如图(1),求∠EOF的度数;
(2)当∠AOB绕点O逆时针旋转至图(2)的位置(0°<∠BOC<90°)时,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2007年5月19日起,中国人民银行上调存款利率.
人民币存款利率调整表:
项 目 | 调整前年利率% | 调整后年利率% |
活期存款 | 0.72 | 0.72 |
二年期定期存款 | 2.79 | 3.06 |
储户的实得利息收益是扣除利息税后的所得利息,利息税率为20%.
(1)小明于2007年5月19日把3500元的压岁钱按一年期定期存入银行,到期时他实得利息收益是多少元?
(2)小明在这次利率调整前有一笔一年期定期存款,到期时按调整前的年利率2.79%计息,本金与实得利息收益的和为2555.8元,问他这笔存款的本金是多少元?
(3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
约定:①存款天数按整数天计算,一年按360天计算利息.
②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存,利息按调整前的一年期定期利率计算;如果转存,转存前已存天数的利息按活期利率计算,转存后,余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com