【题目】按要求解一元二次方程
（1）4x2﹣8x+1=0（配方法） （2）7x（5x+2）=6（5x+2）（因式分解法）
（3）3x2+5（2x+1）=0（公式法） （4）x2﹣2x﹣8=0．
【答案】(1) x1=1+
，x2=1﹣
．(2) x1=﹣
，x2=
；(3) x1=
，x2=
；(4) x1=﹣4，x2=2．
【解析】试题分析：（1）利用配方法解方程.(2)利用因式分解法（提取公因式）解方程.(3)利用公式法解方程.
(4)利用因式分解法（十字相乘）解方程.
试题解析：
解：（1）4x2﹣8x+1=0（配方法）
移项得，x2﹣2x=
，
配方得，x2﹣2x+1=
+1，
（x﹣1）2=
，
∴x﹣1=±
∴x1=1+
，x2=1﹣
．
（2）7x（5x+2）=6（5x+2）（因式分解法）
7x（5x+2）﹣6（5x+2）=0，
（5x+2）（7x﹣6）=0，
∴5x+2=0，7x﹣6=0，
∴x1=﹣
，x2=
；
（3）3x2+5（2x+1）=0（公式法）
整理得，3x2+10x+5=0
∵a=3，b=10，c=5，b2﹣4ac=100﹣60=40，
∴x=
=
，
∴x1=
，x2 =
.
（4）x2﹣2x﹣8=0．
（x+4）（x﹣2）=0，
∴x+4=0，x﹣2=0，
∴x1=﹣4，x2=2．
科目：初中数学 来源： 题型：
【题目】一张如图1的长方形铁皮，四个角都剪去边长为30厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2，铁盒底面长方形的长是4a（cm），宽是3a（cm），这个无盖铁盒各个面的面积之和称为铁盒的全面积．
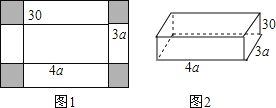
（1）请用a的代数式表示图1中原长方形铁皮的面积；
（2）若要在铁盒的各个外表面漆上某种油漆，每元钱可漆的面积为
（cm2），则油漆这个铁盒需要多少钱（用a的代数式表示）？
（3）铁盒的底面积是全面积的几分之几（用a的代数式表示）？若铁盒的底面积是全面积的
，求a的值；
（4）是否存在一个正整数a，使得铁盒的全面积是底面积的正整数倍？若存在，请求出这个a，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连接OM、ON.
（1）求图①中∠MON的度数；
（2）图②中∠MON的度数是_________，图③中∠MON的度数是___________；
（3）试探究∠MON的度数与正n边形边数n的关系（直接写出答案）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于
的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
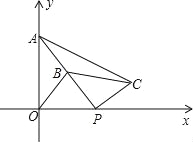
【题目】如图，在平面直角坐标系中，点A的坐标为（0，2），点P（t，0）在x轴上，B是线段PA的中点．将线段PB绕着点P顺时针方向旋转90°，得到线段PC，连结OB、BC．
（1）判断△PBC的形状，并简要说明理由；
（2）当t＞0时，试问：以P、O、B、C为顶点的四边形能否为平行四边形？若能，求出相应的t的值？若不能，请说明理由；
（3）当t为何值时，△AOP与△APC相似？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线y=kx+b与反比例函数y=
（x＞0）的图象分别交于点 A（m，3）和点B（6，n），与坐标轴分别交于点C和点D．
（1）求直线AB的解析式；
（2）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，在平面直角坐标系
中，一次函数
的图象与
轴交于点
，与
轴交于点
，点
的坐标为
，连接
．
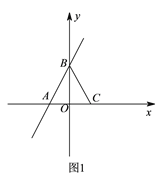
（）求证：
是等边三角形．
（
）点
在线段的延长线上，连接
，作的垂直平分线，垂足为点
，并与轴交于点
，分别连接
、
．
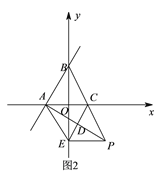
①如图，若
，直接写出
的度数．
②若点在线段的延长线上运动（与点不重合），的度数是否变化？若变化，请说明理由；若不变，求出的度数．
（
）在（）的条件下，若点从点出发在的延长线上匀速运动，速度为每秒个单位长度，
与交于点，设
的面积为
，
的面积为
，
，运动时间为
秒时．求关于
的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y1=
x+m与y轴交于点A（0，6），直线l2：y2=kx+1分别与x轴交于点B（-2，0），与y轴交于点C．两条直线相交于点D，连接AB．
（1）求两直线交点D的坐标；
（2）求△ABD的面积；
（3）根据图象直接写出y1＞y2时自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示为一机器零件的三视图.
（1）请写出符合这个机器零件形状的几何体的名称.
（2）若俯视图中三角形为正三角形，那么请根据图中所标的尺寸，计算这个几何体的表面积（单位：cm2）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com