
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于48棵,且用于购买这两种树的资金不能超过7500元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
【答案】(1)购买A种树苗每棵需100元,购买B种树苗每棵需50元;(2)购买的方案有:购进A种树苗48棵,B种树苗52棵; 购进A种树苗49棵,B种树苗51棵;购进A种树苗50棵,B种树苗50棵;(3)购进A种树苗48棵,B种树苗52棵所付工钱最少,最少工钱为2480元.
【解析】
(1)设![]() 种树苗每棵
种树苗每棵![]() 元,
元,![]() 种树苗每棵
种树苗每棵![]() 元,根据“购买
元,根据“购买![]() 种树苗8棵,
种树苗8棵,![]() 种树苗3棵,需要950元;若购买
种树苗3棵,需要950元;若购买![]() 种树苗5棵,
种树苗5棵,![]() 种树苗6棵,则需要800元”列二元一次方程组求解可得;
种树苗6棵,则需要800元”列二元一次方程组求解可得;
(2)设购进![]() 种树苗
种树苗![]() 棵,则购进
棵,则购进![]() 种树苗
种树苗![]() 棵,根据“
棵,根据“![]() 种树苗不能少于48棵,且用于购买这两种树苗的资金不能超过7500元”列不等式组求解可得;
种树苗不能少于48棵,且用于购买这两种树苗的资金不能超过7500元”列不等式组求解可得;
(3)根据(2)中所得方案,分别计算得出费用即可.
解:(1)(1)设![]() 种树苗每棵
种树苗每棵![]() 元,
元,![]() 种树苗每棵
种树苗每棵![]() 元,
元,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:![]() 种树苗每棵100元,
种树苗每棵100元,![]() 种树苗每棵50元;
种树苗每棵50元;
(2)设购进A种树苗m棵,则购进B种树苗(100﹣m)棵,
根据题意,得: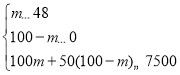 ,
,
解得:48≤m≤50,
所以购买的方案有:
1、购进A种树苗48棵,B种树苗52棵;
2、购进A种树苗49棵,B种树苗51棵;
3、购进A种树苗50棵,B种树苗50棵;
(3)方案1的费用为48×30+52×20=2480元,
方案2的费用为49×30+51×20=2490元,
方案3的费用为50×30+50×20=2500元,
所以购进A种树苗48棵,B种树苗52棵所付工钱最少,最少工钱为2480元.


科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
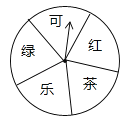
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
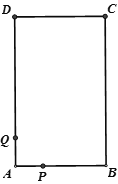
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.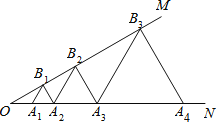
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
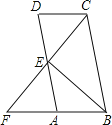
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,在△ACM,△CBN中,AC=CM,BC=CN,∠ACM=∠BCN=60°,连接AN交CM于点E,连接BM交CN于点F.
求证:(1)AN=BM.(2)△CEF是等边三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
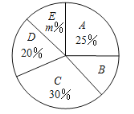
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
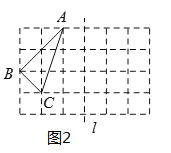
【题目】(1)如图②,利用网格线画![]() ,使它与
,使它与![]() 关于直线
关于直线![]() 对称.若每个小正方形边长为1,则
对称.若每个小正方形边长为1,则![]() 的面积为__.
的面积为__.
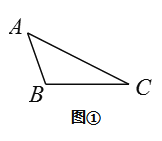
(2)如图①,用直尺和圆规在△ABC的一边![]() 上确定一点
上确定一点![]() ,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com