
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
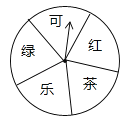
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与该顾客经过两次“有效随机转动”后,获得一瓶可乐的情况,再利用概率公式求解即可求得答案.
试题解析:(1)∵转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;∴一次“有效随机转动”可获得“乐”字的概率为:![]() ;
;
(2)画树状图得:
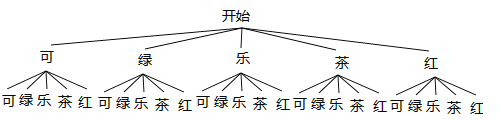
∵共有25种等可能的结果,该顾客经过两次“有效随机转动”后,获得一瓶可乐的有2种情况,∴该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率为:![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]()
![]() ,并且
,并且![]() 满足
满足![]() .一动点
.一动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动;动点
移动;动点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,点
运动,点![]() 分别从点
分别从点![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() (秒)
(秒)

(1)求![]() 两点的坐标;
两点的坐标;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形?并求出此时
是平行四边形?并求出此时![]() 两点的坐标.
两点的坐标.
(3)当![]() 为何值时,
为何值时,![]() 是以
是以![]() 为腰的等腰三角形?并求出此时
为腰的等腰三角形?并求出此时![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.

(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与应用:
观察下列各式:
1+3= 2
1+3+5= 2
1+3+5+7= 2
1+3+5+7+9= 2
……
问题:(1)在横线上填上适当的数;
(2)写出一个能反映此计算一般规律的式子;
(3)根据规律计算:(﹣1)+(﹣3)+(﹣5)+(﹣7)+…+(﹣2019).(结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种蔬菜![]() 千克,不加工直接出售每千克可卖
千克,不加工直接出售每千克可卖![]() 元;如果经过加工重量减少了20%,价格增加了40%,回答下列问题.
元;如果经过加工重量减少了20%,价格增加了40%,回答下列问题.
(1)![]() 千克这种蔬菜不加工直接出售可卖_______元.
千克这种蔬菜不加工直接出售可卖_______元.
(2)![]() 千克这种蔬菜加工后可卖多少元.
千克这种蔬菜加工后可卖多少元.
(3)现有这种蔬菜800千克,不加工直接出售每千克可卖1.5元,那么加工后原800千克这种蔬菜可卖多少元?比加工前多卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图


请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
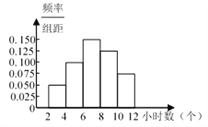
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com