
【题目】如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.

(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
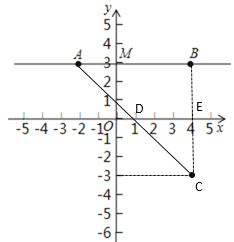
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
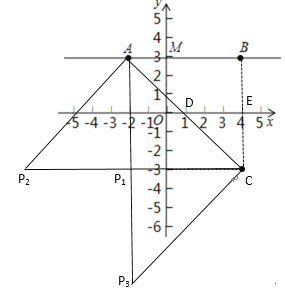
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
【答案】(1)点C见解析,B(4,3),C(4,-3); (2)△ABC 是等腰直角三角形,点 D(1,0); (3)存在点 P,使得△ ACP 是等腰直角三角形,点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).
【解析】
(1)根据点C与点B关于x轴对称描出点C即可得坐标;
(2)根据点坐标求出线段AB、BC的长度,依据∠ABC=90即可确定△ABC是等腰直角三角形,然后求出DE=CE=3可得点D的坐标;
(3)分三种情况作出图形,进而确定点P的坐标即可.
解:(1)如图,可知点B(4,3),C(4,-3);
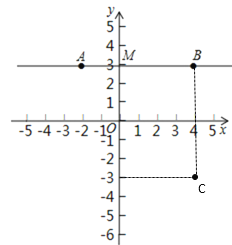
(2)如图,
∵B(4,3),
∴AB=6,
∵C(4,-3),BC⊥x轴,
∴BC=6,
∴AB=BC,∠ABC=90,
∴△ABC是等腰直角三角形,
设BC交x轴于点E,则∠DEC=90,OE=4,
∵∠DCE=45,
∴DE=CE=3,
∴OD=OE-DE=4-3=1,
∴D(1,0);
(3))存在点 P,使得△ACP 是等腰直角三角形,如图,
①当∠APC是直角时,P1(-2,-3);
②当∠PAC是直角时,P2(-8,-3);
③当∠PCA是直角时,P3(-2,-9),
故点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数![]() 、b在数轴上的位置如图所示,
、b在数轴上的位置如图所示,
![]()
(1) a+b 0 , a-b 0; (填“>”、“=”或“<”)
(2) 化简:|a|-|b|+|a-b|
(3)在数轴上表示a+b与a-b;并把![]() 、b、0、a+b、a-b按从小到的顺序用“<”连接起来。
、b、0、a+b、a-b按从小到的顺序用“<”连接起来。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在![]() 轴上,记为
轴上,记为![]() ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是![]() ,与
,与![]() 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.
(1)求OC长度;
(2)求点![]() 的坐标;
的坐标;
(3)求矩形ABCO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=6,E是BC边的中点,F是CD边上的一点,且DF=2,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人到泉州市移动通讯营业厅办理手机通话业务,营业员给他提供了两种办理方式,甲方案:月租9元,每分钟通话费0.2元;乙方案:月租0元,每分钟通话费0.3元.
(1)若此人每月平均通话x分钟,则两种方式的收费各是多少元?(用含x的代数式表示)
(2)此人每月平均通话10小时,选择哪种方式比较合算?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
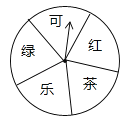
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,∠BAC=120°,AB=AC=6,点D为边BC上一动点.将△ABD沿着AD对折到△AB′D.若△BB′D为直角三角形,则BD=___________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com