【题目】如图，在直角坐标系中放入一个矩形纸片ABCO，将纸片翻折后，点B恰好落在
轴上，记为
，折痕为CE．直线CE的关系式是
，与轴相交于点F，且AE＝3．
（1）求OC长度；
（2）求点的坐标；
（3）求矩形ABCO的面积．
【答案】（1）8； （2）点B/的坐标为（0，6）；（3）80．
【解析】分析：（1）在直线y=-
x+8中令x=0可求得C点坐标，则可求得OC长度；（2）由折叠的性质可求得B′E，在Rt△AB′E中，可求得AB′，再由点E在直线CF上，可求得E点坐标，则可求得OA长，利用线段和差可求得OB′，则可求得点B′的坐标；（3）由（1）、（2）可求得OC和OA，可求得矩形ABCO的面积．
本题解析：（1）∵ 直线
与
轴交于点为C ∴ 令
，则
∴ 点C（0，8） ∴ OC＝8
（2）在矩形OABC中，AB＝OC＝8，∠A＝90° ∵ AE＝3 ∴ BE＝AB－BE＝8－3＝5
∵是△CBE沿CE翻折得到的 ∴ EB/＝BE＝5
在Rt△AB/E中，＝
∵ 点E在直线上，∴ 设E（
，3） ∴ 
∴ 
∴ OA＝10 ∴ OB/＝OA－AB/＝10－4＝6 ∴ 点B/的坐标为（0，6）
（3）由（1），（2）知OC＝8，OA＝10 ∴ 矩形ABCO的面积为：OC×OA＝8×10＝80.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】把（+5）﹣（+3）﹣（﹣1）+（﹣4）写成省略括号的和的形式是（ ）
A.﹣5﹣3+1﹣4
B.5﹣3﹣1﹣4
C.5﹣3+1﹣4
D.5+3+1﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如右图，在△ABC中，点Q，P分别是边AC，BC上的点，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四个结论：①AP平分∠BAC；②AS=AR；③BP=QP；④QP∥AB．其中一定正确的是( )
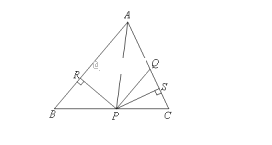
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠BAD=∠CAE=90o，AB=AD，AE=AC， AF⊥CF，垂足为F.
（1）若AC=10，求四边形ABCD的面积；
（2）求证：AC平分∠ECF；
（3）求证：CE=2AF .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知地球上海洋面积为316 000 000km2 ， 数据316 000 000用科学记数法表示为（ ）
A.3.61×109
B.3.61×108
C.3.61×107
D.3.61×106
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请仔细阅读下面材料，然后解决问题：
在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”．例如： 
， 
；当分子的次数小于分母的次数时，我们称之为“真分式”，例如： 
， 
．我们知道，假分数可以化为带分数，例如： 
，类似的，假分式也可以化为“带分式”（整式与真分式和的形式），例如： 
．
（1）将分式
化为带分式；
（2）当x取哪些整数值时，分式
的值也是整数？
（3）当x的值变化时，分式
的最大值为 ．
【答案】（1）2+
；（2）x=0，2，﹣2，4；（3）
.
【解析】试题分析：（1）仿照阅读材料中的方法加你个原式变形即可；
（2）原式变形后，根据结果为整数确定出整数x的值即可；
（3）原式变形后，确定出分式的最大值即可．
试题解析:（1）原式=
=2+
；
（2）由（1）得： 
=2+
，
要使
为整数，则
必为整数，
∴x﹣1为3的因数，
∴x﹣1=±1或±3，
解得：x=0，2，﹣2，4；
（3）原式=
=2+
，
当x2=0时，原式取得最大值
．
故答案为： 
.
【题型】解答题
【结束】
28
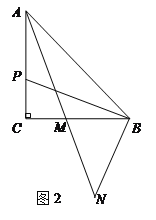
【题目】已知，△ABC中,AC＝BC,∠ACB＝90°，点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90°得线段BN，AN交直线BC于M．
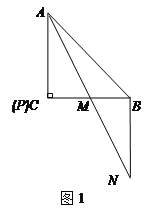
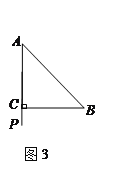
(1)图1，若点P与点C重合，则
＝______,
＝______．(直接写出结果)
(2)图2，若点P在线段AC上，求证: AP＝2MC；
(3)图3，若点P在线段AC的延长线上，完成图形,并直接写出
＝______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
