【题目】解方程：（1）
（2）x2－2x－4＝0
（3）x2﹣4x+1=0（用配方法） （4）
【答案】（1）x1=2，x2=﹣1；（2）x1=1+
，x2=1﹣
；（3）x1=2+
，x2=2﹣
；（4）x1=3，x2=1
【解析】试题分析：（1）移项后开方，即可得出两个一元一次方程，求出方程的解即可；
（2）求出b2﹣4ac的值，再代入公式求出即可；
（3）移项，配方，开方，即可得出两个一元一次方程，求出方程的解即可；
（4）先分解因式，即可得出两个一元一次方程，求出方程的解即可．
试题解析：（1）（2x﹣1）2﹣9=0，
（2x﹣1）2=9，
2x﹣1=±3，
x1=2，x2=﹣1；
（2）x2﹣2x﹣4=0
b2﹣4ac=（﹣2）2﹣4×1×（﹣4）=20，
x=
，
x1=1+
，x2=1﹣
；
（3）x2﹣4x+1=0，
x2﹣4x=﹣1，
x2﹣4x+4=﹣1+4，
（x﹣2）2=3，
x﹣2=
，
x1=2+
，x2=2﹣
；
（4）（x﹣3）2+2x（x﹣3）=0，
（x﹣3）（x﹣3+2x）=0，
x﹣3=0，x﹣3+2x=0，
x1=3，x2=1．
科目：初中数学 来源： 题型：
【题目】在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（﹣1，2）．
（1）把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1；
（2）画出与△A1B1C1关于y轴对称的△A2B2C2；
（3）若点P（a，b）是△ABC边上任意一点，P2是△A2B2C2边上与P对应的点，写出P2的坐标为 ；
（4）试在y轴上找一点Q(在图中标出来)，使得点Q到B2、C2两点的距离之和最小，并求出QB2+QC2的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
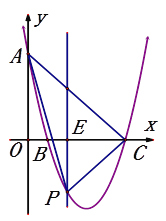
【题目】在平面直角坐标系中，抛物线
与y轴的交点为A，与x轴的正半轴分别交于点B（b，0），C（c，0）.
（1）当b=1时，求抛物线相应的函数表达式；
（2）当b=1时，如图，E（t，0）是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P．求△APC面积的最大值；
（3）当c =b+ n.时，且n为正整数.线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中放入一个矩形纸片ABCO，将纸片翻折后，点B恰好落在
轴上，记为
，折痕为CE．直线CE的关系式是
，与轴相交于点F，且AE＝3．
（1）求OC长度；
（2）求点的坐标；
（3）求矩形ABCO的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一条公路的转弯处是一段圆弧AB．
（1）作出弧AB所在圆的圆心O；（用直尺和圆规作图，保留作图痕迹，不写作法）
（2）若弧AB的中点C到弦AB的距离为20m，AB=80m，求弧AB所在圆的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面．
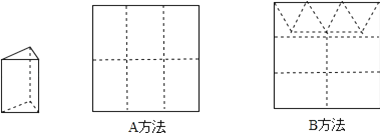
现有19张硬纸板，裁剪时x张用A方法，其余用B方法．
（1）设裁剪出的侧面个数为
个，裁剪出底面的个数为
个.分别求出
、
与x的关系式.
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com