
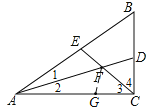
【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

【答案】(1)FE=FD (2)答案见解析
【解析】
(1)先在AC上截取AG=AE,连结FG,利用SAS判定△AEF≌△AGF,得出∠AFE=∠AFG,FE=FG,再利用ASA判定△CFG≌△CFD,得到FG=FD,进而得出FE=FD;
(2)先过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,根据已知条件得到∠GEF=∠HDF,进而判定△EGF≌△DHF(AAS),即可得出FE=FD.也可以过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,再判定△EFG≌△DFH(ASA),进而得出FE=FD.
(1)FE与FD之间的数量关系为:FE=FD.
理由:如图,在AC上截取AG=AE,连结FG,
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△AEF与△AGF中
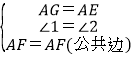 ,
,
∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG,
∵∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,
∴2∠2+2∠3+∠B=180°,
∴∠2+∠3=60°,
又∵∠AFE为△AFC的外角,
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°,
∴∠CFG=180°-60°-60°=60°,
∴∠GFC=∠DFC,
在△CFG与△CFD中,
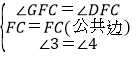 ,
,
∴△CFG≌△CFD(ASA),
∴FG=FD,
∴FE=FD;
(2)结论FE=FD仍然成立.
如图,过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,
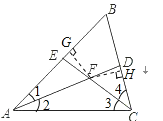
∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=∠1+∠2+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH,
又∵∠HDF=∠B+∠1=60°+∠1,
∴∠GEF=∠HDF,
在△EGF与△DHF中,
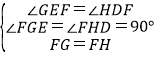 ,
,
∴△EGF≌△DHF(AAS),
∴FE=FD.


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() .将
.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() .连结
.连结![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是正三角形;④
是正三角形;④![]() 的面积为90.其中正确的是______(填所有正确答案的序号).
的面积为90.其中正确的是______(填所有正确答案的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
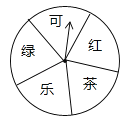
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
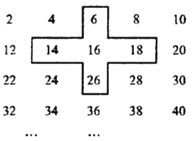
【题目】将连续的偶数2,4,6,8,…,如图所示排列:
(1)求图中十字框内5个数的和与中间的数16的倍数关系.
(2)若将十字框上下左右移动,可框住另外的五个数,请说明这五个数的和与十字框最中间的数之间存在的关系.
(3)若将十字框上下左右移动,框住的五个数的和能等于2019吗?若能,请写出这五个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 | 答对题数 | 答错题数 | 得分 |
小明 | 10 | 10 | 40 |
小红 | 19 | 1 | 94 |
小刚 | 20 | 0 | 100 |
小强 | 18 | 2 | 88 |
小丽 | 14 | 6 | 64 |
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB、CD 是圆O 的两条直径,且∠AOD =α(0° < α < 90°),点P是扇形AOD内任意一点.点P将AB、CD所在直线依次轮流作为对称轴翻折,将点P关于AB对称的点记为点P1 ,点P1关CD 对称的点记为点P2,点 P2 关于AB 对称的点记为点P3,….
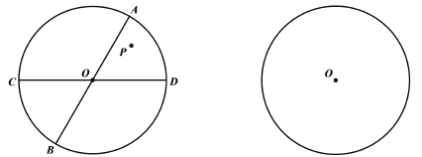
(1)根据所给图中点P 的位置,分别画出点 P 1、P 1;(不写作图步骤,但要保留作图痕迹)
(2)分别联结OP、OP1、OP2,那么线段OP、OP1、OP2 之间的数量关系是:OP OP1 OP2(填空,不要求写出过程);
(3)由(1)、(2)可知,点 P 绕点O旋转可以到达点P2的位置,如果 α=60°,OP= a,求线段 OP顺时针旋转到OP2 过程中扫过的面积;
(4)在 α 取某些特定值的时候,如果按照这样的方式翻折,总能得到一点Pn与点P 重合, 求当n =12,点 P12 与点P 第一次重合时 α 的值.(直接写出结果,不要求写出过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com