练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】列方程解应用题

    学校给七年级学生组织知识竞赛，共设20道题，各题的分值相同，每题必答.下表记录了5名学生的得分情况

    参赛者

    答对题数

    答错题数

    得分

    小明

    10

    10

    40

    小红

    19

    1

    94

    小刚

    20

    0

    100

    小强

    18

    2

    88

    小丽

    14

    6

    64

    (1)参赛者小芳得76分，她答对了几道题？

    (2)参赛者小花说她得了83分，你认为可能吗？为什么？

    【答案】(1)小芳答对了16道题；(2)小花不可能的83分，理由见解析.

    【解析】

    根据表格得出答对一题得5分，再算出错一题扣1分，

    （1）设小芳答对了m道题，答错了（20-m）道题，根据答对的得分+加上答错的得分=76分建立方程求出其解即可；

    （2）假设小花得83分可能，设答对了y道题，答错了（20-y）道题，根据答对的得分+加上答错的得分=83分建立方程求出其解即可．

    由小刚可得答对一题得5分

    设答错一题得x分，10x+50=40(或19×5+x=94或18×5+2x=88或14×5+6x=64)

    x=-1

    (1)设小芳答对了m道题，则答错(20-m)道题

    5m-(20-m)=76

    m=16

    答小芳答对了16道题

    (2)不可能.

    假设可能，设小花答对了y道题，则答错了(20-y)道题

    5y-(20-y)=83

    y=

    因为不是整数

    所以假设不成立

    所以小花不可能的83分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图 ，已知B C=90 ，AEED，ABCE ，点F是AD的中点．说明EF与AD垂直的理由．

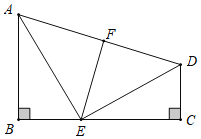
    解：因为 AEED （已知），

    所以AED=90 （垂直的意义）．

    因为AECBBAE （ ），

    即AEDDECBBAE ．

    又因为B=90 （已知），

    所以BAECED （等式性质）．

    在△ ABE 与△ ECD 中，

    BC（已知），ABEC（已知），BAECED，

    所以△ ABE≌△ECD （ ），

    得 （ 全等三角形的对应边相等），

    所以△AED 是等腰三角形．

    因为 （已知），

    所以 EFAD （ ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究与应用：

    观察下列各式：

    1+3＝　 　2

    1+3+5＝　 　2

    1+3+5+7＝　 　2

    1+3+5+7+9＝　 　2

    ……

    问题：（1）在横线上填上适当的数；

    （2）写出一个能反映此计算一般规律的式子；

    （3）根据规律计算：（﹣1）+（﹣3）+（﹣5）+（﹣7）+…+（﹣2019）．（结果用科学记数法表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.

    (1)请你判断并写出FE与FD之间的数量关系(不需证明);

    (2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一种蔬菜千克，不加工直接出售每千克可卖元；如果经过加工重量减少了20%，价格增加了40%，回答下列问题.

    (1)千克这种蔬菜不加工直接出售可卖_______元.

    (2)千克这种蔬菜加工后可卖多少元.

    (3)现有这种蔬菜800千克，不加工直接出售每千克可卖1.5元，那么加工后原800千克这种蔬菜可卖多少元？比加工前多卖多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，

    （1）写出数轴上点B所表示的数　 　；

    （2）点P所表示的数　 　；（用含t的代数式表示）；

    （3）M是AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，说明理由；若不变，请你画出图形，并求出线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校积极开展“阳光体育进校园”活动，决定开设 A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目，规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目，设计了以下四种调查方案.

    方案一：调查该校七年级女生喜欢的运动项目

    方案二：调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目

    方案三：调查该校书法小组的学生喜欢的运动项目

    方案四：调查该校田径队的学生喜欢的运动项目

    （1）上面的调查方案最合适的是 ；

    学校体育组采用了（1）中的方案，将调查的结果绘制成如下两幅不完整的统计图表.

    最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图

    请你结合图表中的信息解答下列问题：

    （2）这次抽样调查的总人数是 ，m＝ ；

    （3）在扇形统计图中，A 项目对应的圆心角的度数为 ；

    （4）已知该校有 1200 名学生，请根据调查结果估计全校学生最喜欢乒乓球的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程．

    （1）2（x﹣2）﹣3（4x﹣1）＝9（1﹣x）；

    （2）；

    （3）；

    （4）；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算：

    （2）计算：（2+）（2﹣）+÷+

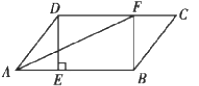
    （3）在ABCD中，过点D作DE⊥AB于点E，点F在CD上且DF＝BE，连接AF，BF．

    ①求证：四边形BFDE是矩形；

    ②若CF＝6，BF＝8，AF平分∠DAB，则DF＝　 　．

    查看答案和解析>>

    同步练习册答案