Question

【题目】如图 ，已知B C=90 ，AEED，ABCE ，点F是AD的中点．说明EF与AD垂直的理由．

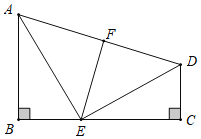
解：因为 AEED （已知），

所以AED=90 （垂直的意义）．

因为AECBBAE （ ），

即AEDDECBBAE ．

又因为B=90 （已知），

所以BAECED （等式性质）．

在△ ABE 与△ ECD 中，

BC（已知），ABEC（已知），BAECED，

所以△ ABE≌△ECD （ ），

得 （ 全等三角形的对应边相等），

所以△AED 是等腰三角形．

因为 （已知），

所以 EFAD （ ）．

Answer 1

【答案】见解析.

【解析】

证出∠BAE=∠CED，证明△ABE ≌△ECD，得出AE=DE，可知△AED是等腰三角形，由等腰三角形的三线合一性质即可得出结论.

因为AE ED（已知），

所以AED=90（垂直的意义），

因为AEC B BAE（ 三角形的一个外角等于与它不相邻的两个内角的和），

即AED DEC B BAE，

又因为B=90（已知），

所以BAE CED（等式性质）．

在△ABE与△ECD 中，

B C（已知），AB EC（已知），BAE CED，

所以△ABE≌△ECD（ASA）．

得AE ED（全等三角形对应边相等）．

所以△AED 是等腰三角形．

因为点F是AD的中点（已知），

所以EF AD（等腰三角形的三线合一）．