
【题目】如图,△ABC是一块直角三角框,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角框内部,将圆形纸片沿着三角框的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,则圆心O运动的路径长为_____.

【答案】15+![]()
【解析】分析:添加如图所示辅助线,圆心O的运动路径长为![]() ,先求出
,先求出![]() 的三边长度,得出其周长,证四边形OEDO1,四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,四边形OECF为正方形,得出
的三边长度,得出其周长,证四边形OEDO1,四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,四边形OECF为正方形,得出![]() 从而知
从而知![]() 利用相似三角形的性质即可得出答案.
利用相似三角形的性质即可得出答案.
详解:如图,圆心O的运动路径长为![]() ,
,

过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D. F.G,
过点O作OE⊥BC,垂足为点E,连接O2B,
过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,
在Rt△ABC中, ![]()
∴
∴![]()
∵O1D⊥BC、O1G⊥AB,
∴D、G为切点,
∴BD=BG,
在Rt△O1BD和Rt△O1BG中,
∵![]()
∴△O1BD≌△O1BG(HL),
∴![]()
在Rt△O1BD中, ![]()
∴
∴![]()
∵O1D=OE=2,O1D⊥BC,OE⊥BC,
∴O1D∥OE,且O1D=OE,
∴四边形OEDO1为平行四边形,
∵![]()
∴四边形OEDO1为矩形,
同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,
又OE=OF,
∴四边形OECF为正方形,
∵![]()
∴![]()
又∵![]()
∴![]()
同理, ![]()
∴△OO1O2∽△CBA,
∴![]() 即
即![]()
∴![]() 即圆心O运动的路径长为
即圆心O运动的路径长为![]() .
.
故答案为: ![]()


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某校举办了一次趣味数学党赛,满分100分,学生得分均为整数,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100
乙组:50,60,60,60,70,70,70,70,80,90.
组别 | 平均分 | 中位数 | 方差 |
甲组 | 68 | a | 376 |
乙组 | b | 70 |
(1)以生成绩统计分析表中a=_________分,b=_________分.
(2)小亮同学说:“这次赛我得了70分,在我们小组中属中游略偏上!”双察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由。
(3)计算乙组成的方差,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会进择哪一组?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=![]() BC,求线段PQ的长.
BC,求线段PQ的长.
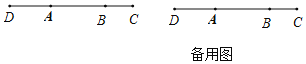
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)若![]() 为等腰直角三角形.
为等腰直角三角形.
①求直线![]() 的函数解析式;
的函数解析式;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
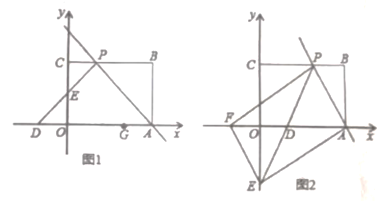
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形![]() 放入平面直角坐标系
放入平面直角坐标系![]() 中,使
中,使![]() 分别落在
分别落在![]() 轴的正半轴上,其中
轴的正半轴上,其中![]() ,对角线
,对角线![]() 所在直线解析式为
所在直线解析式为![]() ,将矩形
,将矩形![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 上的
上的![]() 处.
处.

(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的长度;
的长度;
(3)点![]() 是
是![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() 使得
使得![]() 的周长最小,若存在,请求出点
的周长最小,若存在,请求出点![]() 的坐标,如不存在,请说明理由.
的坐标,如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小李乘坐汽车从上海出发区苏州探望奶奶,全程88千米;返回时,因为另选了行车路线,全程为74千米。已知小李去时的平均速度是返回的1.1倍,所用时间却比返回时多了5分钟,求小李返回时所乘汽车的平均速度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像过点
的图像过点![]() 和点
和点![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角△ABC,使
为边在第一象限内作等腰直角△ABC,使![]()

(1)求一次函数的解析式;
(2)求出点![]() 的坐标
的坐标
(3)点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
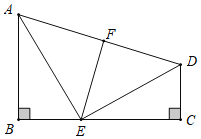
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com