
【题目】(1)计算:![]()
(2)计算:(2+![]() )(2﹣
)(2﹣![]() )+
)+![]() ÷
÷![]() +
+![]()
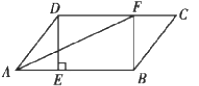
(3)在ABCD中,过点D作DE⊥AB于点E,点F在CD上且DF=BE,连接AF,BF.
①求证:四边形BFDE是矩形;
②若CF=6,BF=8,AF平分∠DAB,则DF= .
【答案】(1)7(2)![]() (3)①详见解析;②10
(3)①详见解析;②10
【解析】
(1)按顺序先利用完全平方公式展开,进行二次根式的化简,进行平方运算,然后再按运算顺序进行计算即可;
(2)按顺序先利用平方差公式进行展开,进行二次根式的除法,进行负指数幂的运算,然后再按运算顺序进行计算即可;
(3)①先证明四边形DEBF是平行四边形,然后再根据有一个角是直角的平行四边形是矩形即可得结论;
②先利用勾股定理求出BC长,再根据平行四边形的性质可得AD长,再证明DF=AD即可得.
(1)原式=2+2![]() +1-2
+1-2![]() +4
+4
=7;
(2)原式=4-3+![]() +4
+4
=5+![]() =
=![]() ;
;
(3)①∵四边形ABCD是平行四边形,
∴AB//CD,即BE//DF,
又∵DF=BE,
∴四边形DEBF是平行四边,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四边形BFDE是矩形;
②∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
∴BC=![]() =10,
=10,
∵四边形ABCD是平行四边形,
∴AD=BC=10,AB//CD,
∴∠FAB=∠DFA,
∵∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴DF=AD=10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 | 答对题数 | 答错题数 | 得分 |
小明 | 10 | 10 | 40 |
小红 | 19 | 1 | 94 |
小刚 | 20 | 0 | 100 |
小强 | 18 | 2 | 88 |
小丽 | 14 | 6 | 64 |
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
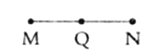
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB、CD 是圆O 的两条直径,且∠AOD =α(0° < α < 90°),点P是扇形AOD内任意一点.点P将AB、CD所在直线依次轮流作为对称轴翻折,将点P关于AB对称的点记为点P1 ,点P1关CD 对称的点记为点P2,点 P2 关于AB 对称的点记为点P3,….
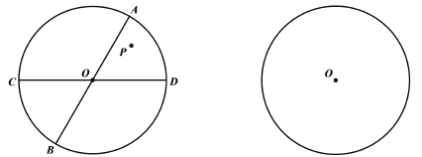
(1)根据所给图中点P 的位置,分别画出点 P 1、P 1;(不写作图步骤,但要保留作图痕迹)
(2)分别联结OP、OP1、OP2,那么线段OP、OP1、OP2 之间的数量关系是:OP OP1 OP2(填空,不要求写出过程);
(3)由(1)、(2)可知,点 P 绕点O旋转可以到达点P2的位置,如果 α=60°,OP= a,求线段 OP顺时针旋转到OP2 过程中扫过的面积;
(4)在 α 取某些特定值的时候,如果按照这样的方式翻折,总能得到一点Pn与点P 重合, 求当n =12,点 P12 与点P 第一次重合时 α 的值.(直接写出结果,不要求写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C三地在同一条路上,A地在B地的正南方3千米处,甲、乙两人分别从A、B两地向正北方向的目的地C匀速直行,他们分别和A地的距离s(千米)与所用的时间t(小时)的函数关系如图所示.

(1)图中的线段l1是 (填“甲”或“乙”)的函数图象,C地在B地的正北方向 千米处;
(2)谁先到达C地?并求出甲乙两人到达C地的时间差;
(3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达C地,求他提速后的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A、点B是直线l上的两点,AB=36厘米,点C在线段AB上,且AC=![]() AB,点P、点Q分别从点C、点B同时朝点A方向运动,且点P、点Q运动的速度分别为2厘米/秒、4厘米/秒,若点M是PQ的中点,则经过_____秒时线段AM的长为18厘米.
AB,点P、点Q分别从点C、点B同时朝点A方向运动,且点P、点Q运动的速度分别为2厘米/秒、4厘米/秒,若点M是PQ的中点,则经过_____秒时线段AM的长为18厘米.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com