
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
【答案】C
【解析】
连接AH,由四边形ABCD是正方形与点E、F、H分别是AB、BC、CD的中点,容易证得△BCE≌△CDF与△ADH≌△DCF,根据全等三角形的性质,容易证得CE⊥DF与AH⊥DF,故①正确;根据垂直平分线的性质,即可证得AG=AD,继而AG=DC,而DG≠DC,所以AG≠DG,故②错误;由直角三角形斜边上的中线等于斜边的一半,即可证得HG=![]() DC,∠CHG=2∠GDC,根据等腰三角形的性质,即可得∠DAG=2∠DAH=2∠GDC.所以∠DAG=∠CHG,④正确,则问题得解.
DC,∠CHG=2∠GDC,根据等腰三角形的性质,即可得∠DAG=2∠DAH=2∠GDC.所以∠DAG=∠CHG,④正确,则问题得解.

∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E. F. H分别是AB、BC、CD的中点,
∴BE=FC
∴△BCE≌△CDF,
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故①正确;
连接AH,
同理可得:AH⊥DF,
∵CE⊥DF,
∴△CGD为直角三角形,
∴HG=HD=![]() CD,
CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD=DC,
在Rt△CGD中,DG≠DC,
∴AG≠DG,故②错误;
∵AG=AD, AH垂直平分DG
∴∠DAG=2∠DAH,
根据①,同理可证△ADH≌△DCF
∴∠DAH=∠CDF,
∴∠DAG=2∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠GHC=∠DAG,故③正确,
所以①和③正确选择C.


科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图


请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
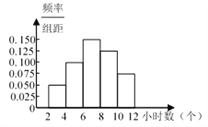
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]()
(2)计算:(2+![]() )(2﹣
)(2﹣![]() )+
)+![]() ÷
÷![]() +
+![]()
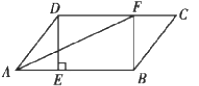
(3)在ABCD中,过点D作DE⊥AB于点E,点F在CD上且DF=BE,连接AF,BF.
①求证:四边形BFDE是矩形;
②若CF=6,BF=8,AF平分∠DAB,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() 的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —
的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —![]() >0的解集是___________.
>0的解集是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
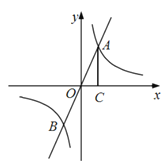
【题目】如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
(1)求反比例函数的表达式;
(2)点B的坐标为 ;
(3)当![]() 时,直接写出x的取值范围。
时,直接写出x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
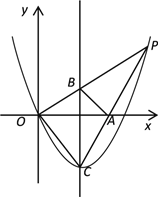
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com