
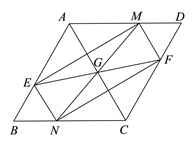
【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:
(1)由已知条件易得∠EAG=∠FCG,AG=GC结合∠AGE=∠FGC可得△EAG≌△FCG,从而可得△EAG≌△FCG,由此可得EG=FG,同理可得MG=NG,由此即可得到四边形ENFM是平行四边形;
(2)如下图,由四边形ENFM为矩形可得EG=NG,结合AG=CG,∠AGE=∠CGN可得△EAG≌△NCG,则∠BAC=∠ACB ,AE=CN,从而可得AB=CB,由此可得BE=BN.
详解:
(1)∵四边形ABCD为平行四四边形边形,
∴AB//CD.
∴∠EAG=∠FCG.
∵点G为对角线AC的中点,
∴AG=GC.
∵∠AGE=∠FGC,
∴△EAG≌△FCG.
∴EG=FG.
同理MG=NG.
∴四边形ENFM为平行四边形.
(2)∵四边形ENFM为矩形,
∴EF=MN,且EG=![]() ,GN=
,GN=![]() ,
,
∴EG=NG,
又∵AG=CG,∠AGE=∠CGN,
∴△EAG≌△NCG,
∴∠BAC=∠ACB ,AE=CN,
∴AB=BC,
∴AB-AE=CB-CN,
∴BE=BN.


科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
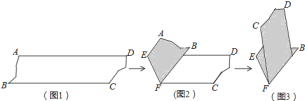
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() (m为常数)
(m为常数)
(1)求证:不论m为何值,方程总有两个不相等的实数根;
(2)若方程有一个根是2,求m的值及方程的另一个根。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com