
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
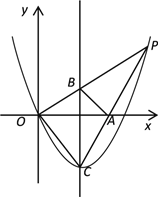
【答案】(1) y=x2-2x;(2)BC=m-1;(3) P的坐标为(![]() )
)
【解析】分析:(1)由对称轴公式,以及已知顶点C坐标,利用待定系数法确定出解析式即可;
(2)设出P坐标,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N,表示出PN,ON,OM,利用比例表示出BM,进而表示出BC即可;
(3)设出P坐标,由两三角形面积相等得到AC=AP,过点P作PQ⊥BC交BC于点Q,列出关于t的方程,求出方程的解确定出t的值,即可求出P坐标.
详解:(1)∵抛物线y=ax2+bx的顶点为C(1,﹣1),∴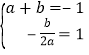 ,解得:
,解得:![]() ,∴抛物线的表达式为:y=x2﹣2x;
,∴抛物线的表达式为:y=x2﹣2x;
(2)∵点P的横坐标为m,∴点P的纵坐标为:m2﹣2m,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N.∵P是抛物线上位于第一象限内的一点,∴PN=m2﹣2m,ON=m,OM=1,由![]() =
=![]() ,得:
,得:![]() =
=![]() ,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
(3)令P(t,t2﹣2t).∵△ABP的面积等于△ABC的面积,∴AC=AP,过点P作PQ⊥BC交BC于点Q,∴CM=MQ=1,可得:t2﹣2t=1,解得:t=1+![]() (t=1﹣
(t=1﹣![]() 舍去),∴P的坐标为(1+
舍去),∴P的坐标为(1+![]() ,1).
,1).



科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段AB=1=0﹣(﹣1);线段 BC=2=2﹣0;线段 AC=3=2﹣(﹣1)问题
①数轴上点M、N代表的数分别为﹣9和1,则线段MN= ;
②数轴上点E、F代表的数分别为﹣6和﹣3,则线段EF= ;
③数轴上的两个点之间的距离为5,其中一个点表示的数为2,则另一个点表示的数为m,求m.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A、点B是直线l上的两点,AB=36厘米,点C在线段AB上,且AC=![]() AB,点P、点Q分别从点C、点B同时朝点A方向运动,且点P、点Q运动的速度分别为2厘米/秒、4厘米/秒,若点M是PQ的中点,则经过_____秒时线段AM的长为18厘米.
AB,点P、点Q分别从点C、点B同时朝点A方向运动,且点P、点Q运动的速度分别为2厘米/秒、4厘米/秒,若点M是PQ的中点,则经过_____秒时线段AM的长为18厘米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
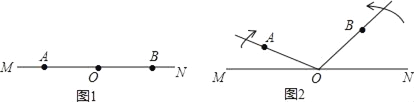
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
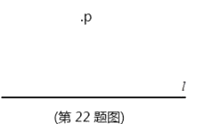
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com