
【题目】有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个B.2个C.3个D.4个
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
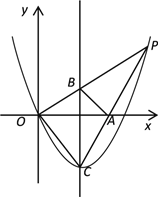
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:

(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶15分钟后,甲、乙两人相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
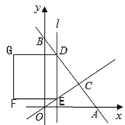
【题目】如图,直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,4),平行于
交于点C(2,4),平行于![]() 轴的直线
轴的直线![]() 从原点
从原点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向右平移,直线
轴向右平移,直线![]() 分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线
分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线![]() 经过点A时停止运动,设直线
经过点A时停止运动,设直线![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)![]()
(2)设线段DE的长度为![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当正方形DEFG的边GF落在![]() 轴上,求出
轴上,求出![]() 的值;
的值;
(4)当![]() 时,若正方形DEFG和△OCB重叠部分面积为4,则
时,若正方形DEFG和△OCB重叠部分面积为4,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学为了解自己居住的小区家庭生活用水情况,从中随机调查了其中![]() 的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
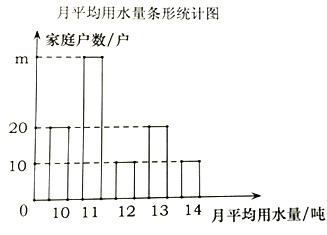
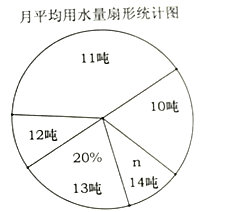
![]() 小明随机调查了 户家庭,该小区共有 户家庭;
小明随机调查了 户家庭,该小区共有 户家庭;
![]()
![]() ,
,![]() ;
;
![]() 这个样本数据的众数是 ,中位数是 ;
这个样本数据的众数是 ,中位数是 ;
![]() 根据样本数据,请估计该小区家庭月平均用水量不超过
根据样本数据,请估计该小区家庭月平均用水量不超过![]() 吨的有多少户?
吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
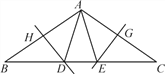
A. ![]() B. AD,AE将∠BAC三等分
B. AD,AE将∠BAC三等分
C. △ABE≌△ACD D. S△ADH=S△CEG
【答案】A
【解析】试题解析:∵∠B=∠C=36°,∴AB=AC,∠BAC=108°,∵DH垂直平分AB,EG垂直平分AC,∴DB=DA,EA=EC,∴∠B=∠DAB=∠C=∠CAE=36°,∴△BDA∽△BAC,∴![]() ,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则
,又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,∴∠ADC=∠DAC,∴CD=CA=BA,∴BD=BC﹣CD=BC﹣AB,则![]() =
=![]() ,即
,即![]() =
=![]() ,故A错误;
,故A错误;
∵∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,∴∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,∴AD,AE将∠BAC三等分,故B正确;
∵∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,∴∠BAE=∠CAD,在△BAE和△CAD中,∵∠B=∠C,AB=AC,∠BAE=∠CAD,∴△BAE≌△CAD,故C正确;
由△BAE≌△CAD可得S△BAE=S△CAD,即S△BAD+S△ADE=S△CAE+S△ADE,∴S△BAD=S△CAE,又∵DH垂直平分AB,EG垂直平分AC,∴S△ADH=![]() S△ABD,S△CEG=
S△ABD,S△CEG=![]() S△CAE,∴S△ADH=S△CEG,故D正确.
S△CAE,∴S△ADH=S△CEG,故D正确.
故选A.
【题型】单选题
【结束】
11
【题目】红细胞是人体中血液运输氧气的主要媒介,人体中红细胞的直径约为0.0000077m,将0.0000077用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
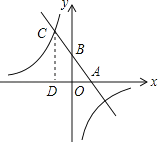
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴交于负半轴,给出六个结论:①a>0;②b>0;③c>0;④a+b+c=0;⑤b2﹣4ac>0;⑥2a﹣b>0,其中正确结论序号是_____.
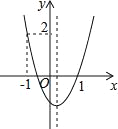
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com