
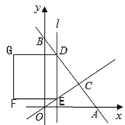
【题目】如图,直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,4),平行于
交于点C(2,4),平行于![]() 轴的直线
轴的直线![]() 从原点
从原点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向右平移,直线
轴向右平移,直线![]() 分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线
分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线![]() 经过点A时停止运动,设直线
经过点A时停止运动,设直线![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)![]()
(2)设线段DE的长度为![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当正方形DEFG的边GF落在![]() 轴上,求出
轴上,求出![]() 的值;
的值;
(4)当![]() 时,若正方形DEFG和△OCB重叠部分面积为4,则
时,若正方形DEFG和△OCB重叠部分面积为4,则![]() 的值为________.
的值为________.
【答案】(1)b=8,k=2;(2)当t<2时,d=-4t+8;当t>2时,d=4x-8;(3)t=![]() ;(4)t=1.
;(4)t=1.
【解析】
(1)直接把点的坐标代入即可;(2)根据正方形性质和函数图象,分两种情况当t<2时;当t>2时;(3)设D(t,-2t+8),E(t,2t),DE=-4t+8;则 t=-4t+8;(4)由t(-4t+8)=4可得t.
解:(1)因为直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,4),
交于点C(2,4),
所以![]() ,
,![]()
解得b=8,k=2;
(2)根据正方形性质,当t<2时,d=-4t+8;
当t>2时,d=4x-8;
(3)设D(t,-2t+8),E(t,2t),DE=-4t+8;
则 t=-4t+8,
解得t=![]() ;
;
(4)由t(-4t+8)=4,解得t=1.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外卖小哥骑车从商家出发,向东骑了3千米到达小林家,继续骑2.5千米到达小红家,然后向西骑了10千米到达小明家,最后返回商家。
(1)以商家为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小林家,小红家的位置。(小林家用点A表示,小红家用点B表示,小明家用点C表示)
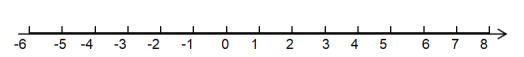
(2)小明家距小林家______千米
(3)若外卖小哥在骑车过程中每千米耗时3分钟,那么外卖小哥在整个过程中共用时多久?(假设外卖小哥一直在匀速行驶,在每户人家上门送外卖的时间忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | |
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
则m= ;
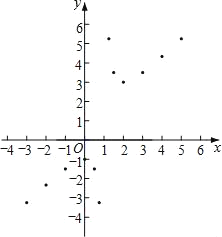
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)该函数的图象关于点( , )成中心对称;
(5)直线y=m与该函数的图象无交点,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如下说法:①直线是一个平角;②如果线段AB=BC,则B是线段AC的中点;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,直线最短;⑥120.5°=120°30′,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
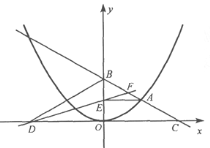
【题目】如图,在平面直角坐标系中,A是抛物线![]() 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交![]() 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当![]() 时,求S的值.
时,求S的值.
(2)求S关于![]() 的函数解析式.
的函数解析式.
(3)①若S=![]() 时,求
时,求![]() 的值;
的值;
②当m>2时,设![]() ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
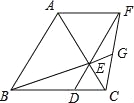
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
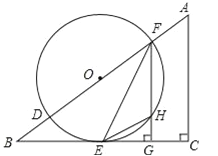
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com