
【题目】已知A、B、C三地在同一条路上,A地在B地的正南方3千米处,甲、乙两人分别从A、B两地向正北方向的目的地C匀速直行,他们分别和A地的距离s(千米)与所用的时间t(小时)的函数关系如图所示.

(1)图中的线段l1是 (填“甲”或“乙”)的函数图象,C地在B地的正北方向 千米处;
(2)谁先到达C地?并求出甲乙两人到达C地的时间差;
(3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达C地,求他提速后的速度.
【答案】(1)乙;3;(2)甲先到达,到达目的地的时间差为![]() 小时;(3)速度慢的人提速后的速度为
小时;(3)速度慢的人提速后的速度为![]() 千米/小时.
千米/小时.
【解析】分析:
(1)根据题意结合所给函数图象进行判断即可;
(2)由所给函数图象中的信息先求出二人所对应的函数解析式,再由解析式结合图中信息求出二人到达C地的时间并进行比较、判断即可得到本问答案;
(3)根据图象中的信息结合(2)中的结论进行解答即可.
详解:
(1)由题意结合图象中的信息可知:图中线段l1是乙的图象;C地在B地的正北方6-3=3(千米)处.
(2)甲先到达.
设甲的函数解析式为s=kt,则有4=t,
∴s=4t.
∴当s=6时,t=![]() .
.
设乙的函数解析式为s=nt+3,则有4=n+3,即n=1.
∴乙的函数解析式为s=t+3.
∴当s=6时,t=3.
∴甲、乙到达目的地的时间差为:![]() (小时).
(小时).
(3)设提速后乙的速度为v千米/小时,
∵相遇处距离A地4千米,而C地距A地6千米,
∴相遇后需行2千米.
又∵原来相遇后乙行2小时才到达C地,
∴乙提速后2千米应用时1.5小时.
即![]() ,解得:
,解得:![]() ,
,
答:速度慢的人提速后的速度为![]() 千米/小时.
千米/小时.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌T恤专营批发店的T恤衫在进价基础上加价m%销售,每月销售额9万元,该店每月固定支出1.7万元,进货时还需付进价5%的其它费用.
(1)为保证每月有1万元的利润,m的最小值是多少?(月利润=总销售额-总进价-固定支
出-其它费用)
(2)经市场调研发现,售价每降低1%,销售量将提高6%,该店决定自下月起降价以促进销售,已知每件T恤原销售价为60元,问:在m取(1)中的最小值且所进T恤当月能够全部销售完的情况下,销售价调整为多少时能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索代数式![]() 与代数式
与代数式![]() 的关系.
的关系.
(1)当![]() ,
,![]() 时,分别计算两个代数式的值.
时,分别计算两个代数式的值.
(2)当![]() ,
,![]() 时,分别计算两个代数式的值.
时,分别计算两个代数式的值.
(3)你发现了什么规律?
(4)利用你发现的规律计算:20182-2×2018×2019+20192.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]()
(2)计算:(2+![]() )(2﹣
)(2﹣![]() )+
)+![]() ÷
÷![]() +
+![]()
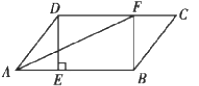
(3)在ABCD中,过点D作DE⊥AB于点E,点F在CD上且DF=BE,连接AF,BF.
①求证:四边形BFDE是矩形;
②若CF=6,BF=8,AF平分∠DAB,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
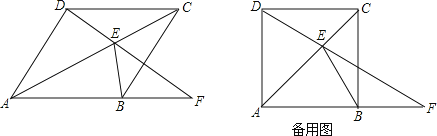
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() 的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —
的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —![]() >0的解集是___________.
>0的解集是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年四月份,某校在孝感市争创“全国文明城市” 活动中,组织全体学生参加了“弘扬孝感文化,争做文明学生”知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成![]() 六个等级,并绘制成如下两幅不完整的统计图表.
六个等级,并绘制成如下两幅不完整的统计图表.


请根据图表提供的信息,解答下列问题:
(1)本次抽样调查样本容量为 ,表中:![]() ,
,![]() ;扇形统计图中,
;扇形统计图中,![]() 等级对应的圆心角
等级对应的圆心角![]() 等于 度;(4分=1分+1分+1分)
等于 度;(4分=1分+1分+1分)
(2)该校决定从本次抽取的![]() 等级学生(记为甲、乙、丙、丁)中,随机选择
等级学生(记为甲、乙、丙、丁)中,随机选择![]() 名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com