【题目】如图，
平分
，
于点
，
于点
，
，则图中全等三角形的对数有______对.
【答案】3
【解析】
由题意可知∠AOP=∠BOP， OP=OP，若加条件OA=OB，由SAS可得△AOP≌△BOP；若加条件
于点
，
于点
，由HL可得Rt△EOP≌Rt△FOP；进一步再由前面的结论得PE=PF，PA=PB，所以Rt△EAP≌Rt△FBP（HL），答案即得.
解：∵OA=OB，∠AOP=∠BOP， OP=OP，∴△AOP≌△BOP（SAS）；
∵于点，于点，∴∠OEP=∠OFP=90°，
又∵∠AOP=∠BOP，OA=OB，∴Rt△EOP≌Rt△FOP（HL）；
∵Rt△EOP≌Rt△FOP，∴PE=PF，
∵△AOP≌△BOP，∴PA=PB，
∴Rt△EAP≌Rt△FBP（HL）；
所以共有3对全等的三角形，故答案为3.
科目：初中数学 来源： 题型：
【题目】小张在自家土地上平整出了一块苗圃，并将这块苗圃分成了四个长方形区域，其尺寸如图所示（图中长度单位：米），小张计划在这四个区域上按图中所示分别种植草本花卉 1 号、2 号、3 号、4 号．
（1）用式子表示这块苗圃的总面积；
（2）已知种植草本花卉 1 号、2 号、3 号、4 号的成本分别是每平方米 4 元、6 元、8 元、10 元．
①用式子表示小张在这块苗圃上种植草本花卉的总成本；
②当 a=9 时，求小张在这块苗圃上种植草本花卉的总成本．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y1=ax2+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点是B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①abc＞0；②方程ax2+bx+c=3有两个相等的实数根；③抛物线与x轴的另一个交点是（﹣1，0）；④当1＜x＜4时，有y2＞y1；⑤x（ax+b）≤a+b，其中正确的结论是 ．（只填写序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
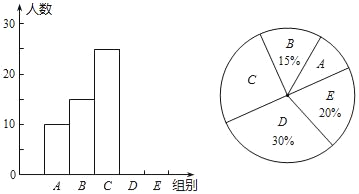
【题目】我校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分．
组别 | 正确数字x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息解决下列问题：
（1）在统计表中，m= ，n= ，并补全条形统计图．
（2）扇形统计图中“C组”所对应的圆心角的度数是 ．
（3）有三位评委老师，每位老师在E组学生完成学校比赛后，出示“通过”或“淘汰”或“待定”的评定结果．学校规定：每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛，请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究与应用：
观察下列各式：
1+3＝ 2
1+3+5＝ 2
1+3+5+7＝ 2
1+3+5+7+9＝ 2
……
问题：（1）在横线上填上适当的数；
（2）写出一个能反映此计算一般规律的式子；
（3）根据规律计算：（﹣1）+（﹣3）+（﹣5）+（﹣7）+…+（﹣2019）．（结果用科学记数法表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知OE是∠AOC的角平分线，OD是∠BOC的角平分线．
（1）若∠AOC=120°，∠BOC=30°，求∠DOE的度数；
（2）若∠AOB=90°，∠BOC=α，求∠DOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，
（1）写出数轴上点B所表示的数 ；
（2）点P所表示的数 ；（用含t的代数式表示）；
（3）M是AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，说明理由；若不变，请你画出图形，并求出线段MN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某品牌T恤专营批发店的T恤衫在进价基础上加价m%销售，每月销售额9万元，该店每月固定支出1.7万元，进货时还需付进价5%的其它费用.
（1）为保证每月有1万元的利润，m的最小值是多少？（月利润＝总销售额－总进价－固定支
出－其它费用）
（2）经市场调研发现，售价每降低1%，销售量将提高6%，该店决定自下月起降价以促进销售，已知每件T恤原销售价为60元，问：在m取（1）中的最小值且所进T恤当月能够全部销售完的情况下，销售价调整为多少时能获得最大利润，最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com