
【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

【答案】(1) 45°;(2) 45°.
【解析】(1)根据角平分线定义,先求∠AOE= ![]() ∠AOC , ∠COD=
∠AOC , ∠COD= ![]() ∠BOC ,
∠BOC ,
由∠DOE=∠AOC-∠AOE -∠COD可求的结果;
(2)根据角平分线定义,得∠AOE= ![]() (90°+α),∠COD=
(90°+α),∠COD= ![]() α ,再根据∠DOE=∠AOC - ∠AOE-∠COD可求得结果.
α ,再根据∠DOE=∠AOC - ∠AOE-∠COD可求得结果.
解:(1)∵ OE是∠AOC的角平分线,OD是∠BOC的角平分线.
∴ ∠AOE= ![]() ∠AOC ,
∠AOC ,
∠COD= ![]() ∠BOC ,
∠BOC ,
∵∠AOC=120°,∠BOC=30°
∴ ∠AOE= ![]() ×120° =60°
×120° =60°
∠COD= ![]() × 30°= 15°
× 30°= 15°
∠DOE=∠AOC - ∠AOE - ∠COD
=120°- 60°-15°= 45°.
(2)∵ ∠AOB=90°,∠BOC=α
∴ ∠AOC = 90°+α
∵ OE是∠AOC的角平分线,OD是∠BOC的角平分线.
∴∠AOE= ![]() ∠AOC , ∠COD=
∠AOC , ∠COD= ![]() ∠BOC
∠BOC
∠AOE= ![]() (90°+α),∠COD=
(90°+α),∠COD= ![]() α
α
∠DOE=∠AOC - ∠AOE-∠COD
= (90°+α)- ![]() (90°+α)-
(90°+α)- ![]() α = 45°
α = 45°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离![]() 有关他这次探究活动的描述错误的是( )
有关他这次探究活动的描述错误的是( )
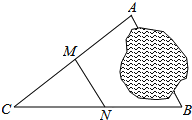
A. ![]() B. CM:CA=1:2 C. MN//AB D. AB=24cm
B. CM:CA=1:2 C. MN//AB D. AB=24cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( ).
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了多少名学生?其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为多少?喜欢“戏曲”活动项目的人数是多少人?
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分 布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求: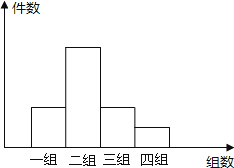
(1)此班这次上交作品共多少件?
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b图象经过点(0,3)和(4,7).
①试求k与b;
②画出这个一次函数图象;
③这个一次函数与x轴交点坐标是_____;
④当x_____时,y<0;
⑤当x_____时,y>0;
⑥当0<y<7时,x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
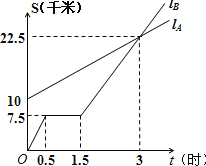
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答.

问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?

(提示:过点P作PE∥AD),请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com