
【题目】问题情境:(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答.

问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?

(提示:过点P作PE∥AD),请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系.

【答案】(1)∠APC=110° ;(2)∠CPD=∠α+∠β , 理由见解析;(3)∠CPD=∠α-∠β 或 ∠CPD=∠β-∠α
【解析】(1)根据平行线的判定与性质填写即可;
(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(3)画出图形(分两种情况①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
(1)过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(平行于同一条直线的两条直线平行)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(两直线平行同旁内角互补)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(等量代换)
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
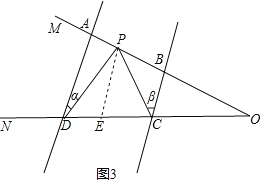
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,
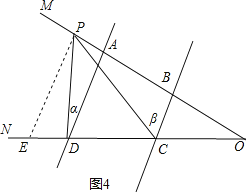
过P作PE∥AD交CD于E,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠β-∠α;
当P在AB延长线时,

同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠α-∠β.


科目:初中数学 来源: 题型:
【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在直角坐标系中,
在直角坐标系中,
![]() 请写出
请写出![]() 各点的坐标.
各点的坐标.
![]() 若把
若把![]() 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到![]() ,写出
,写出![]() 、
、![]() 、
、![]() 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形.
![]() 求出三角形ABC的面积.
求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( ) 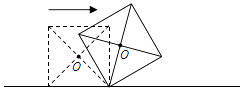
A.4a
B.2 ![]() πa
πa
C.![]() πa
πa
D.![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
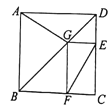
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,点P为BC边上一点,设BP=x,AP2=y(如图1),已知y是x的二次函数的一部分,其图象如图2所示,点Q(2,12)是图象上的最低点.
(1)边AB= , BC边上的高AH=;
(2)当△ABP为直角三角形时,BP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-8,0)及动点P(x,y),且2x-y=-6.设三角形OPA的面积为S.
(1)当x=-2时,点P坐标是____________;
(2)若点P在第二象限,且x为整数时,求y的值;
(3)是否存在第一象限的点P,使得S=12.若存在,求点P的坐标;若不存在,
说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com